选择排序
算法思想:
从序列起始顺序扫描,找出最小的关键字,与第一个关键字交换,然后从剩下的关键字中继续选择最小的关键字,并交换。如此反复,最终使得序列有序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public void selectionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 0; i < arr.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) {
minIndex = arr[j] < arr[minIndex] ? j : minIndex;
}
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
}
|
冒泡排序
算法思想:
将第一个关键字与第二个关键字比较, 如果第一个关键字比第二个关键字大,则二者交换位置,否则不变;第二个关键字与第三个关键字比较,如果第二个关键字比第三个关键字大,则二者交换位置,否则不变…如此反复,一趟排序完成后,最大的关键字会被交换到最后,经过多趟排序即可使序列有序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| public void bubbleSort(int[] arr) {
boolean flag = false;
if (arr == null || arr.length < 2) {
return;
}
for (int i = arr.length; i > 0; --i) {
flag = false;
for (int j = 0; j < i; ++j) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
flag = true;
}
}
if (flag == false) {
return;
}
}
}
|
插入排序
算法思想:
每趟排序中将待排序的关键字按照其值大小插入到已经排好序的部分有序序列的适当位置,直到所有待排关键字都被插入到有序序列中为止。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| public void insertionSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 1; i < arr.length; ++i) {
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; --j) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
|
归并排序
算法思想:
将整个序列分成两半,对每一半进行归并排序,将得到两个有序序列,然后两个有序序列归并成一个序列即可。
merge
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| public void merge(int[] arr, int left, int mid, int right) {
int[] temp = new int[right - left + 1];
int i = 0;
int p1 = left;
int p2 = mid + 1;
while (p1 <= mid && p2 <= right) {
temp[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= mid) {
temp[i++] = arr[p1++];
}
while (p2 <= right) {
temp[i++] = arr[p2++];
}
for (int j = 0; j < temp.length ; j++) {
arr[left + j] = temp[j];
}
}
|
mergeSort
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public void mergeSort(int[] arr, int left, int right) {
if (left == right) {
return;
}
int mid = left + ((right - left) >> 1);
mergeSort(arr, left, mid);
mergeSort(arr, mid + 1, right);
merge(arr, left, mid, right);
}
public void mergeSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
mergeSort(arr, 0, arr.length - 1);
}
|
堆排序
算法思想:
将无序序列调整成大根堆,将堆顶元素与序列最后一个元素交换位置,此时有序序列增加一个,无序序列减少一个,对新的无序序列进行重复操作,即可实现排序。
heapify
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
public void heapify(int[] arr, int index, int size) {
int left = index * 2 + 1;
while (left < size) {
int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;
largest = arr[largest] > arr[index] ? largest : index;
if (largest == index) {
break;
}
int temp = arr[index];
arr[index] = arr[largest];
arr[largest] = temp;
index = largest;
left = index * 2 + 1;
}
}
|
heapSort
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
public void heapSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
int heapSize = arr.length;
for (int i = heapSize / 2; i >= 0; --i) {
heapify(arr, i, heapSize);
}
int size = arr.length;
swap(arr, 0, --size);
while (size > 0) {
heapify(arr, 0, size);
swap(arr, 0, --size);
}
}
public void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
|
快速排序


算法思想:
通过多次枢轴划分实现操作,每趟选择当前所有子序列中的一个关键字作为枢轴,将子序列中比枢轴小的移动到枢轴前面,比枢轴大的移动到枢轴后面,划分结束,继续下一趟划分直到整个序列有序。
partition
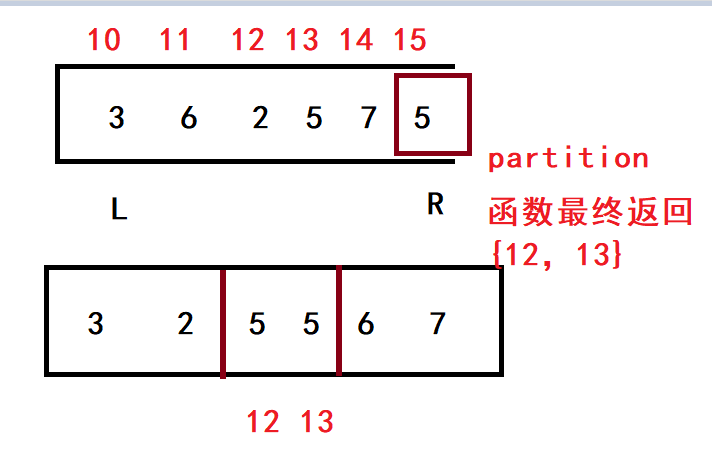
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| public int[] partition(int[] arr, int left, int right) {
int lessZoneRightBoundary = left - 1;
int moreZoneLeftBoundary = right + 1;
while (left < moreZoneLeftBoundary) {
if (arr[left] < arr[right]) {
swap(arr, ++lessZoneRightBoundary, left++);
} else if (arr[left] > arr[right]) {
swap(arr, --moreZoneLeftBoundary, left);
} else {
left++;
}
}
return new int[] {lessZoneRightBoundary + 1 , moreZoneLeftBoundary - 1};
}
|
quickSort
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| public void quickSort(int[] arr, int left, int right) {
if (left < right) {
swap(arr, left + (int)(Math.random() * (right - left + 1)), right);
int[] p = partition(arr, left, right);
quickSort(arr, left, p[0] - 1);
quickSort(arr, p[1] + 1, right);
}
}
public void quickSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
quickSort(arr, 0, arr.length - 1);
}
public void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
|
桶排序
算法思想:
多关键字排序,最低位优先。最低位关键字通过”分配“和”收集“的思想排成若干子序列,再对每个子序列进行更高位排序。
算法图解:
准备若干桶,$count$ 长度为10,$help$ 长度为5,按个位进行词频统计

将个位情况下的 $count$ 数组优化成前缀和形式,原数组表示个位数字的词频,前缀和数组表示个位数小于等于 $i$ 的有arr[i]个

从左向右判断,062的个位数2,小于等于2的词频为4个,所以放在help[3],更新词频

同理,052个位数2,词频3,放在2位置更新词频,011个位数是1,词频是2,放在1位置,更新词频
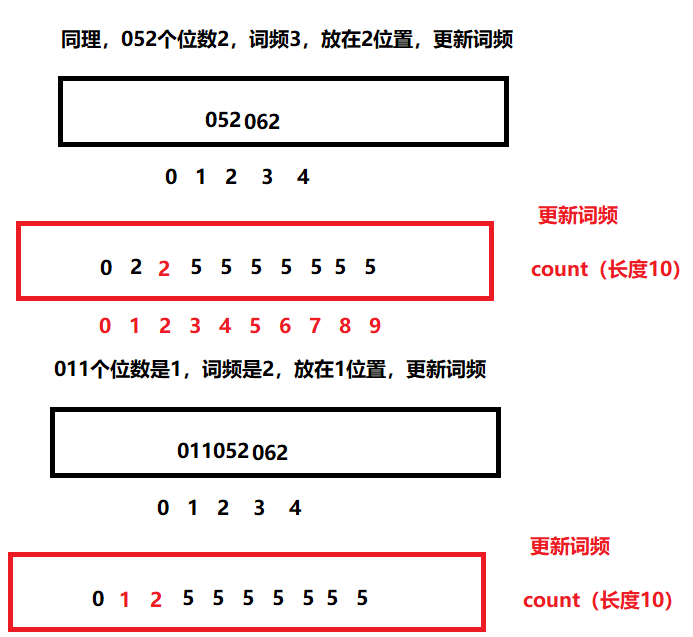
021和013同理,不再赘述。
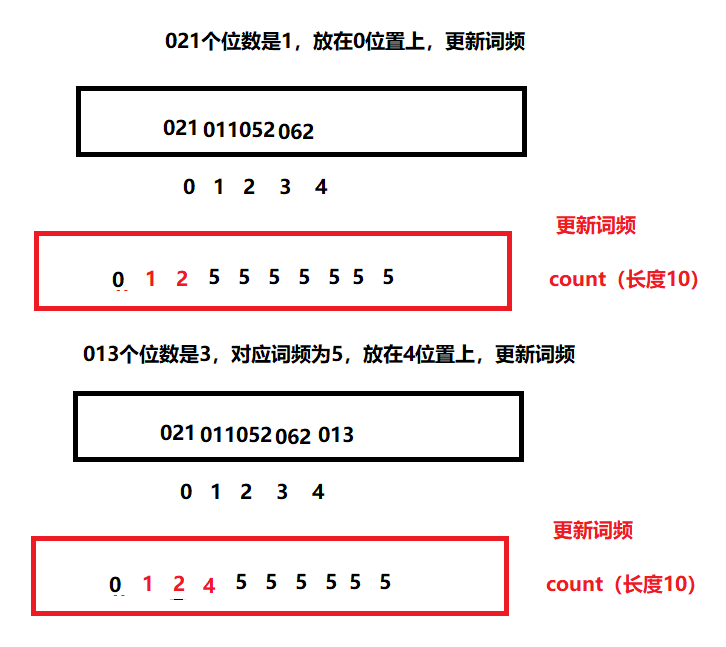
maxbits
1
2
3
4
5
6
7
8
9
10
11
12
13
|
public int maxbits(int[] arr) {
int max = Integer.MIN_VALUE;
for (int i = 0; i < arr.length; i++) {
max = Math.max(max, arr[i]);
}
int res = 0;
while (max != 0) {
res++;
max /= 10;
}
return res;
}
|
getDigit
1
2
3
4
|
public int getDigit(int x, int d) {
return ((x / ((int) Math.pow(10, d - 1))) % 10);
}
|
radixSort
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| public void radixSort(int[] arr, int begin, int end, int digit) {
final int radix = 10;
int i = 0, j = 0;
int[] bucket = new int[end - begin + 1];
for (int d = 1; d <= digit; d++) {
int[] count = new int[radix];
for (i = begin; i <= end; i++) {
j = getDigit(arr[i], d);
count[j]++;
}
for (i = 1; i < radix; i++) {
count[i] = count[i] + count[i - 1];
}
for (i = end; i >= begin; i--) {
j = getDigit(arr[i], d);
bucket[count[j] - 1] = arr[i];
count[j]--;
}
for (i = begin, j = 0; i <= end; i++, j++) {
arr[i] = bucket[j];
}
}
}
public void radixSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
radixSort(arr, 0, arr.length - 1, maxbits(arr));
}
|
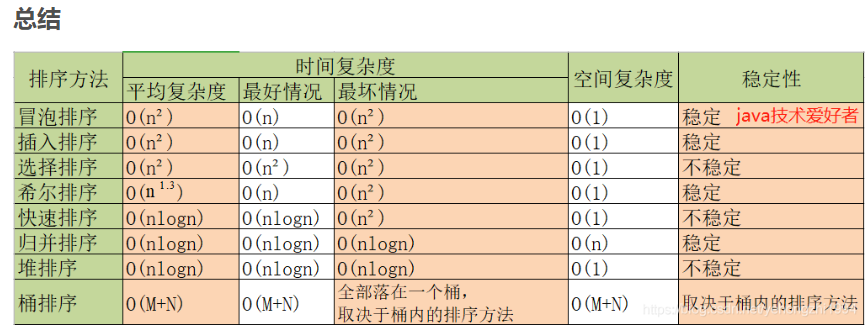
排序总结