算法导学-1-数组类型题目
掌握情况
| 题目 | 通关 |
|---|---|
| 二分查找 | 通过 |
| 移除元素 | 通过 |
| 有序数组的平方 | 通过 |
| 长度最小的子数组 | 未通过 |
| 螺旋矩阵 II |
二分查找
问题
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。1
2
3
4
5
6
7输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
题解
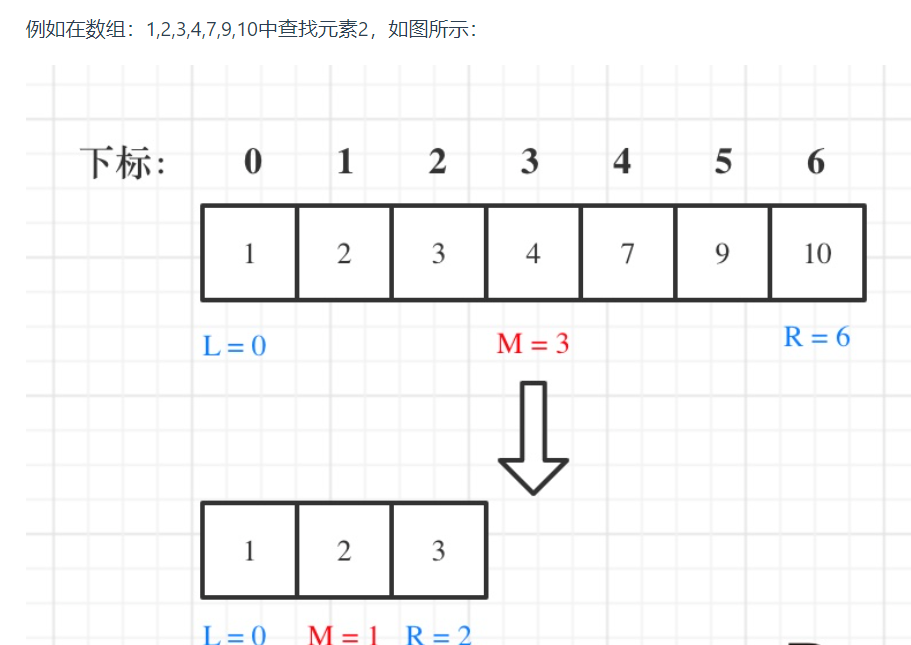
这道题目的前提是数组为有序数组,同时题目还强调数组中无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的,这些都是使用二分法的前提条件
写二分法,区间的定义一般为两种,左闭右闭即[left, right],或者左闭右开即[left, right)。
左闭右闭的区间[left, right]
target在[left, right]区间,所以有如下两点:
- while (left <= right) 要使用 <= ,因为left == right是有意义的,所以使用 <=
- if (nums[middle] > target) right 要赋值为 middle - 1,因为当前这个nums[middle]一定不是target,那么接下来要查找的左区间结束下标位置就是 middle - 1
1 | public int binarySearch(int[] nums, int target) { |
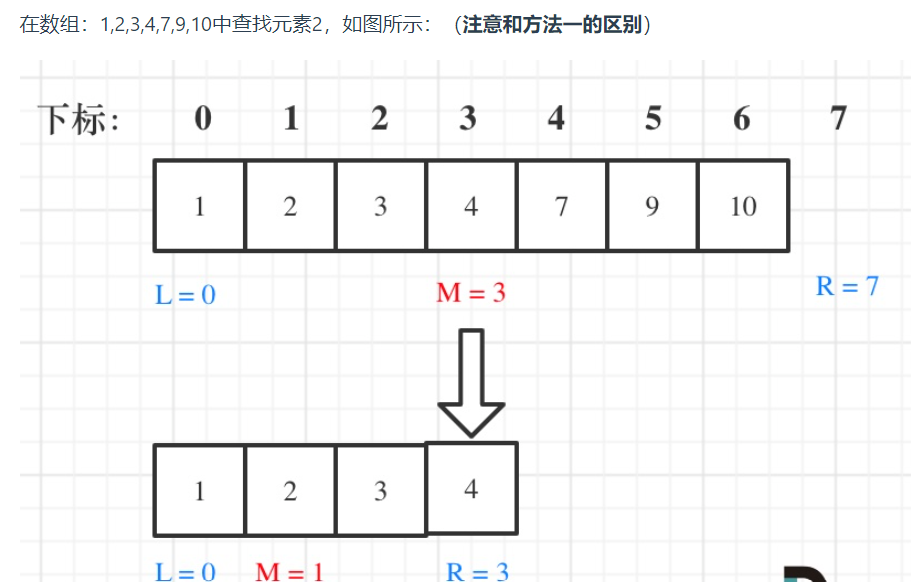
左闭右开的区间[left, right)
- while (left < right),这里使用 <,因为left == right在区间[left, right)是没有意义的
- if (nums[middle] > target) right 更新为 middle,==因为当前nums[middle]不等于target,去左区间继续寻找,而寻找区间是左闭右开区间,所以right更新为middle==,即:下一个查询区间不会去比较nums[middle]
1 | int search(vector<int>& nums, int target) { |
复杂度分析
由于每次查找都会将查找范围缩小一半,因此二分查找的时间复杂度是 O(logn),其中 n是数组的长度。
移除元素
问题
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
双指针法
题解
使用双指针,右指针right指向当前需要处理的元素,左指针left指向下一个将要赋值的位置
如果右指针指向的元素不等于
val,它一定是输出数组的一个元素,则将右指针指向的元素复制到左指针位置,然后同时移动左右指针如果右指针指向的元素等于
val,它不能在输出数组里,此时左指针不动,右指针右移一位
整个过程保持不变的性质是:区间 [0,left) 中的元素都不等于val。当左右指针遍历完输入数组以后,left 的值就是输出数组的长度。
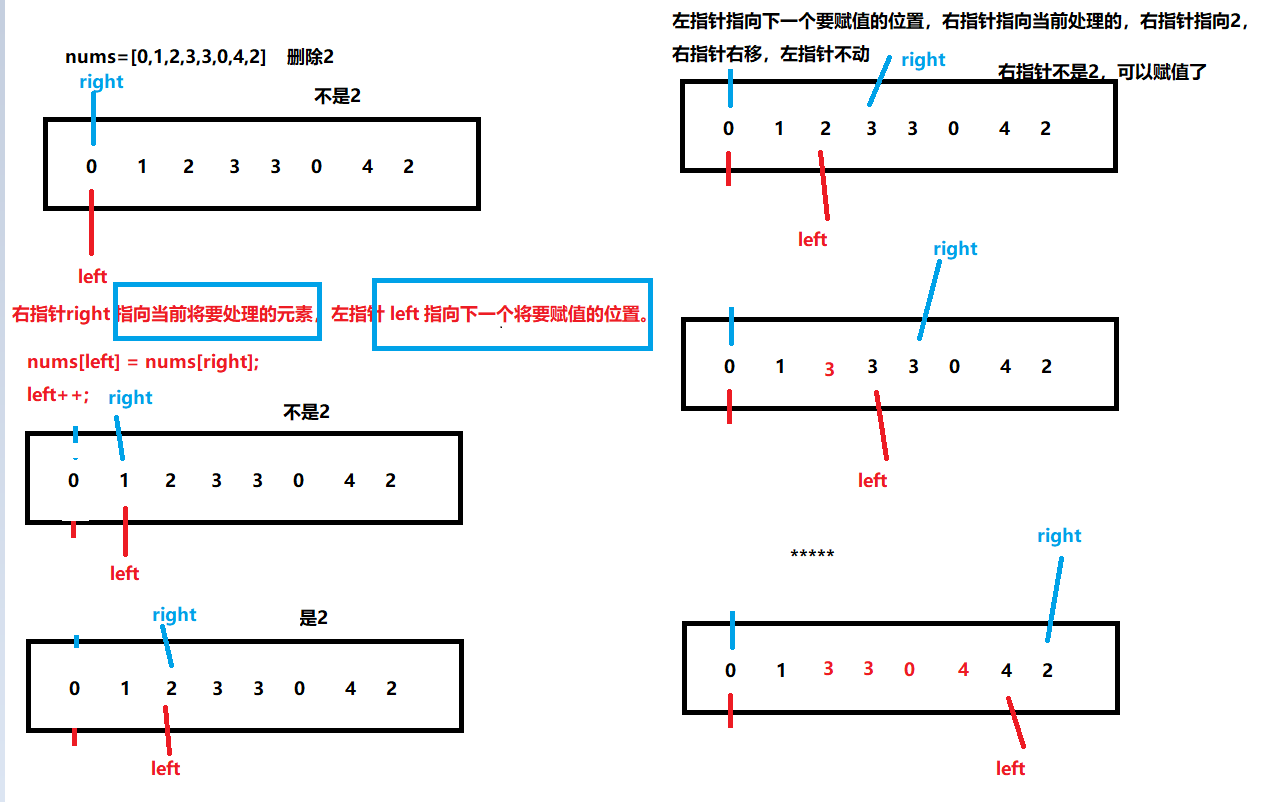
图解
删除2,当左右指针都指向0(左指针指向下一个要赋值的位置,右指针指向当前要处理的元素),此时右指针的值复制到左指针位置,左右指针同时右移,左右指针指向1同理。当左右指针指向到2,此时左指针不动,右指针右移。右指针来到3,不是2,右指针复制到左指针位置,…
1 | public int removeElement(int[] nums, int val) { |
复杂度分析
O(n),其中 n 为序列的长度。我们只需要遍历该序列至多两次, 在最坏情况下(输入数组中没有元素等于val),左右指针各遍历了数组一次。
双指针优化法
题解
如果要移除的元素恰好在数组的开头,例如序列 [1,2,3,4,5],当 val 为 1 时,我们需要把每一个元素都左移一位。注意到题目中说:「元素的顺序可以改变」。实际上我们可以直接将最后一个元素 5 移动到序列开头,取代元素 1,得到序列 [5,2,3,4],同样满足题目要求。这个优化在序列中val 元素的数量较少时非常有效。
实现方面,我们依然使用双指针,两个指针初始时分别位于数组的首尾,向中间移动遍历该序列。
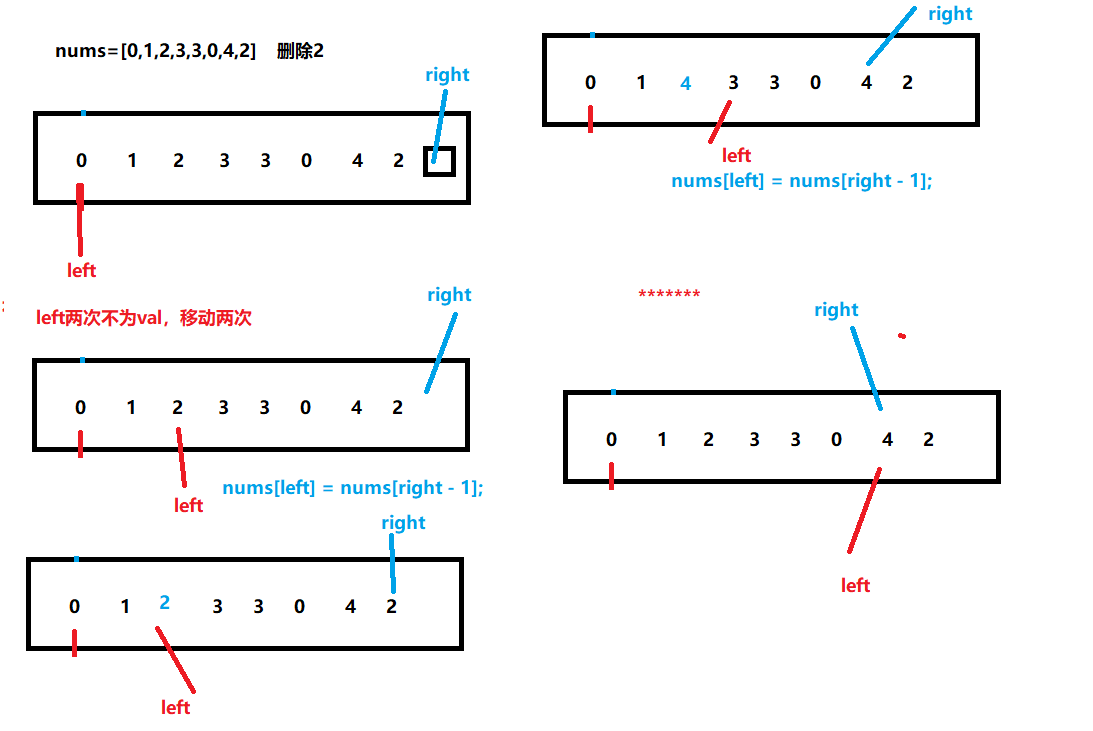
- 如果左指针left 指向的元素等于val,此时将右指针right 指向的元素复制到左指针left 的位置,然后右指针 right 左移一位。
如果赋值过来的元素恰好也等于val,可以继续把右指针right 指向的元素的值赋值过来(左指针 left 指向的等于val 的元素的位置继续被覆盖),直到左指针指向的元素的值不等于 val 为止。
当左指针left 和右指针right 重合的时候,左右指针遍历完数组中所有的元素。
- ==与方法一不同的是,方法二避免了需要保留的元素的重复赋值操作。==
1 | public int removeElement(int[] nums, int val) { |
有序数组的平方
问题
给你一个按非递减顺序排序的整数数组nums,返回每个数字的平方组成的新数组,要求也按非递减顺序排序。
1 | 输入:nums = [-4,-1,0,3,10] |
排序
算法思想:
顺序遍历数组并完成平方操作,然后直接排序操作,排序调用系统API占用时间和空间。
1 | public int[] sortedSquares(int[] nums) { |
双指针+归并排序
算法思想:
- 如果数组 nums 中的所有数都是非负数,那么将每个数平方后,数组仍然保持升序;
- 如果数组nums 中的所有数都是负数,那么将每个数平方后,数组会保持降序。
- 找到数组nums 中负数与非负数的分界线,那么就可以用类似==「归并排序」==的方法了。
- 设neg为数组nums 中负数与非负数的分界线,将数组 nums 中的数平方后,那么 nums[0] 到nums[neg] 单调递减,nums[neg+1] 到 nums[n−1] 单调递增。
- 使用归并的方法进行排序。使用两个指针分别指向位置 neg 和 neg+1,每次比较两个指针对应的数,选择较小的那个放入答案并移动指针。当某一指针移至边界时,将另一指针还未遍历到的数依次放入答案。
1 | // 双指针+归并排序 |
复杂度分析
O(n),其中 n 为数组长度
双指针优化
使用双指针指向首尾,每次比较两个指针对应的数,选择较大的那个逆序放入答案并移动指针。这种方法无需处理某一指针移动至边界的情况
1 | // 双指针 |
长度最小的子数组
问题
给定一个含有n个正整数的数组和一个正整数target。
找出该数组中满足其和≥target的长度最小的连续子数组[numsl, numsl+1, ..., numsr-1, numsr],并返回其长度。如果不存在符合条件的子数组,返回0。
1 | 输入:target = 7, nums = [2,3,1,2,4,3] |
暴力枚举
算法思想:
初始化数组最小长度,美剧数组nums中的每个下标作为子数组的开始下标,对于每个开始下标i,需要找到大于等于i的最小下标j,使得从nums[i]到nums[j]的元素和大于等于s,并更新子数组的最小长度(此时子数组的长度是$j-i+1$)
会出现超时1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22// 暴力枚举
public int minSubArrayLen(int target, int[] nums) {
if (nums.length == 0) {
return 0;
}
int ans = Integer.MAX_VALUE;
// 枚举每个位置的可能性
for (int i = 0; i < nums.length; i++) {
int sum = 0;
// 从i位置作为子数组的开始
for (int j = i; j < nums.length; j++) {
sum += nums[j];
if (sum >= target) {
ans = Math.min(ans, j - i + 1);
break;
}
}
}
return ans == Integer.MAX_VALUE ? 0 : ans;
}
复杂度分析
O(n^2^), 其中 n 是数组的长度。需要遍历每个下标作为子数组的开始下标,对于每个开始下标,需要遍历其后面的下标得到长度最小的子数组。
滑动窗口
算法思想:
定义两个指针start 和end 分别表示子数组(滑动窗口窗口)的开始位置和结束位置,维护变量sum 存储子数组中的元素和(即从nums[start]到nums[end]的元素和)。
- 初始状态下,start 和end 都指向下标 0,sum 的值为 0。
- 每一轮迭代,将
nums[end]加到sum,如果$sum≥target$,则更新子数组的最小长度(此时子数组的长度是 $end−start+1$),然后将nums[start]从sum 中减去并将start右移,直到 $sum<s$,在此过程中同样更新子数组的最小长度。 - 在每一轮迭代的最后,将end 右移。
算法图解
开始时,首尾指针指向2,sum为0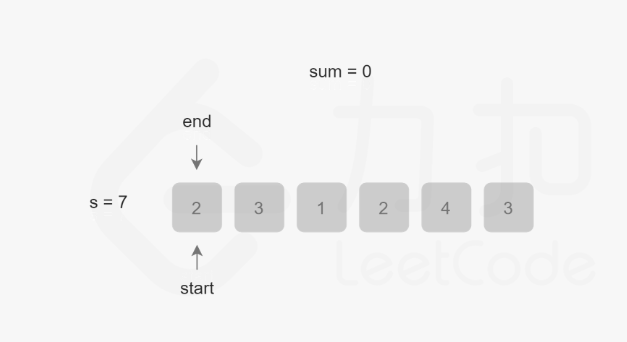
将尾指针元素加入,sum更新为2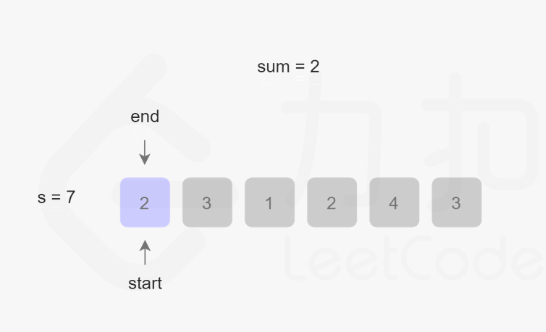
将尾指针元素加入,sum更新为5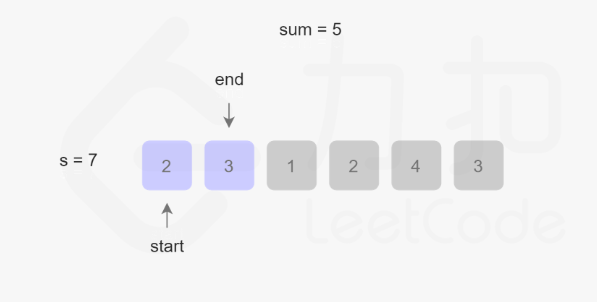
将尾指针元素加入,sum更新为6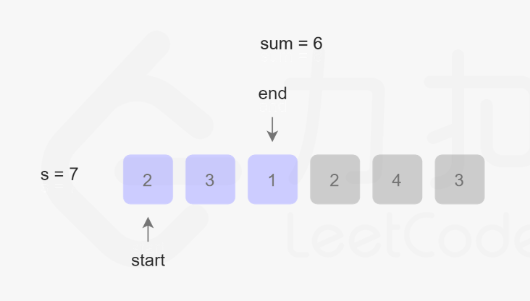
将尾指针元素加入,sum更新为8,由于8>target,ans=4,首指针右移,剔除首元素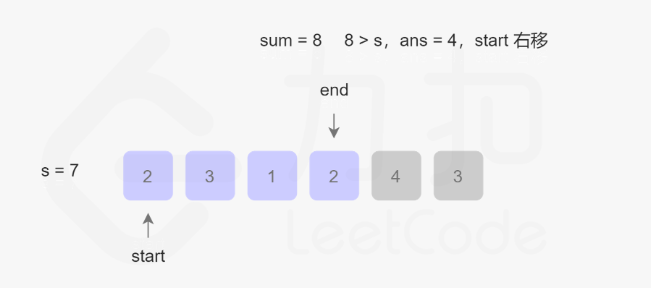
滑动窗口内元素为3、1、2,sum为6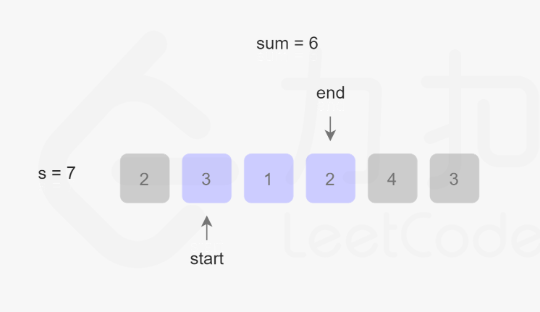
将尾指针元素加入,sum更新为10,10>target,ans=4,首指针右移,剔除首元素3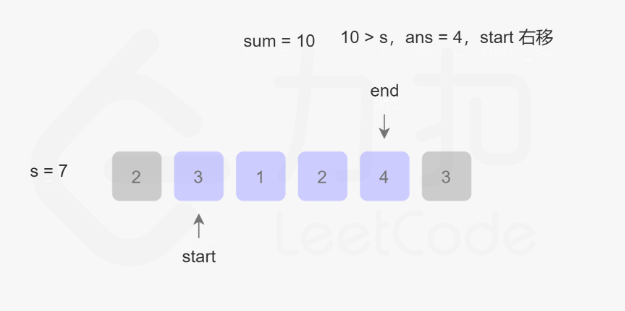
此时sum=7,7=target,ans=3,首指针右移,剔首除元素1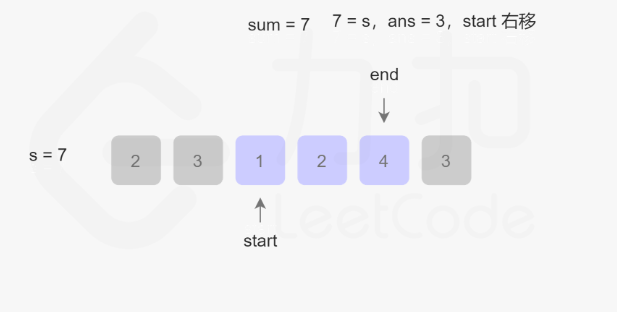
此时sum=6,尾指针准备右移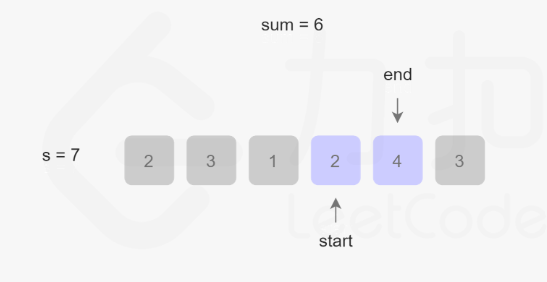
将尾指针元素加入,sum更新为9,9>target,ans=3,首指针右移,剔除首元素2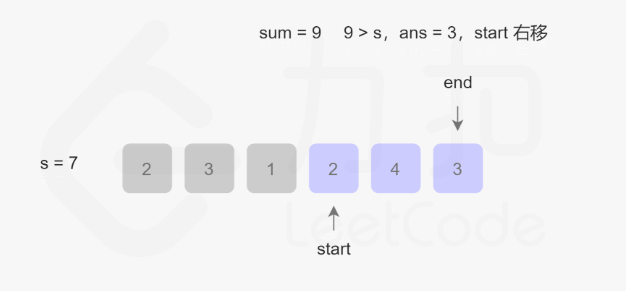
此时sum=7,7=target,ans=2,首指针右移,剔除首元素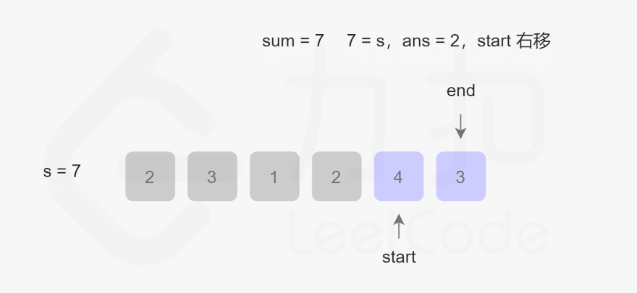
首尾指针来到数组尾部,不满足条件,返回ans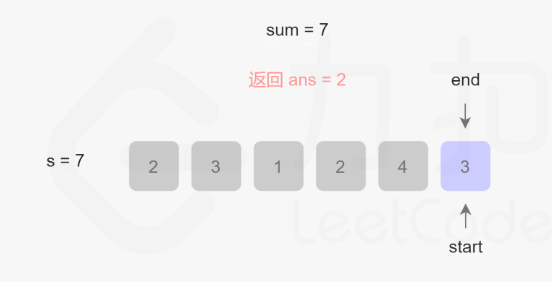
1 | public int minSubArrayLen2(int target, int[] nums) { |
复杂度分析
O(n),其中 n 是数组的长度。指针 start 和 end 最多各移动 n 次。
前缀和+二分查找
算法思想
- 由于要求连续子数组,可以利用前缀和思想。额外创建一个数组sums 用于存储数组 nums 的前缀和,其中
sums[i]表示从nums[0]到nums[i−1]的元素和 - 得到前缀和之后,对于每个开始下标i,可通过二分查找得到大于或等于i 的最小下标bound,使得 $sums[bound]−sums[i−1]≥target$,并更新子数组的最小长度(此时子数组的长度是
bound−(i−1)) - 这道题保证了数组中每个元素都为正,所以前缀和一定是递增的,这一点保证了二分的正确性。如果题目没有说明数组中每个元素都为正,这里就不能使用二分来查找这个位置了。
二分查找大于等于某数的第一个为位置
1 | public int lowerBound(int[] a, int left, int right, int target) { |
1 | // 前缀和+二分查找 |
复杂度分析
需要遍历每个下标作为子数组的开始下标,遍历的时间复杂度是$O(n)$,对于每个开始下标,需要通过二分查找得到长度最小的子数组,二分查找得时间复杂度是$O(logn)$,因此总时间复杂度是 $O(nlogn)$。
螺旋矩阵 II
问题
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。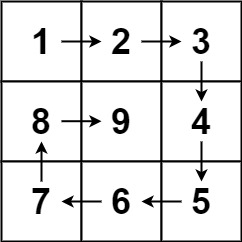
1 | 输入:n = 3 |
全局角度
在矩阵中用左上角的坐标$(tR,tC)$和右下角坐标$(dR,dC)$可以表示一个子矩阵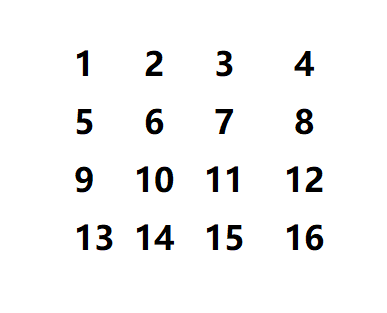

当$(tR,tC)=(0,0)$,$(dR,dC)=(3,3)$时,表示的子矩阵就是整个矩阵,矩阵最外层如上,先把最外层矩阵打印,然后tR++,tC++,dR--,dC--表示的子矩阵如下: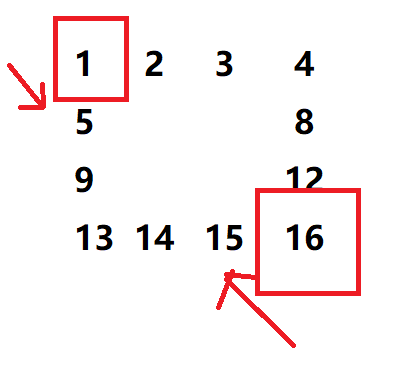
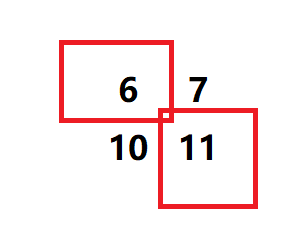
再把内层矩阵打印出来即可,如果发现左上角坐标跑到了右下角坐标的右方或下方,整个过程停止。
1 | // 全局角度 |
复杂度分析
$O(n^2)$,其中 n 是数组的长度
局部角度
1 | public int[][] generateMatrix(int n) { |
数组类型总结
- 二分查找只适用于有序序列并且无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的,这些都是使用二分法的前提条件
- 双指针思想,如
LeetCode 977.有序数组的平方 - 滑动窗口思想,如
LeetCode 209.长度最小的子数组 - 前缀和思想,如
LeetCode 209.长度最小的子数组 - 模拟类型,可以按层整体处理,也可以局部处理,如
LeetCode 59. 螺旋矩阵 II










