归并排序应用1—小和问题

在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组的小和。

1
2
3
4
5
6
7
[1, 3, 4, 2, 5]
1 左边比 1 小的数，没有;
3 左边比 3 小的数，1;
4 左边比 4 小的数，1、3;
2 左边比 2 小的数，1;
5 左边比 5 小的数，1、3、4、 2;
因此小和为 1 + 1 + 3 + 1 + 1 + 3 + 4 + 2 = 16

算法思想：

将左边小于arr[i]的和转换成求arr[i]右边的和，即原问题是求一个数左边比它小，并求和，转换成一个数右边比它大，并求和

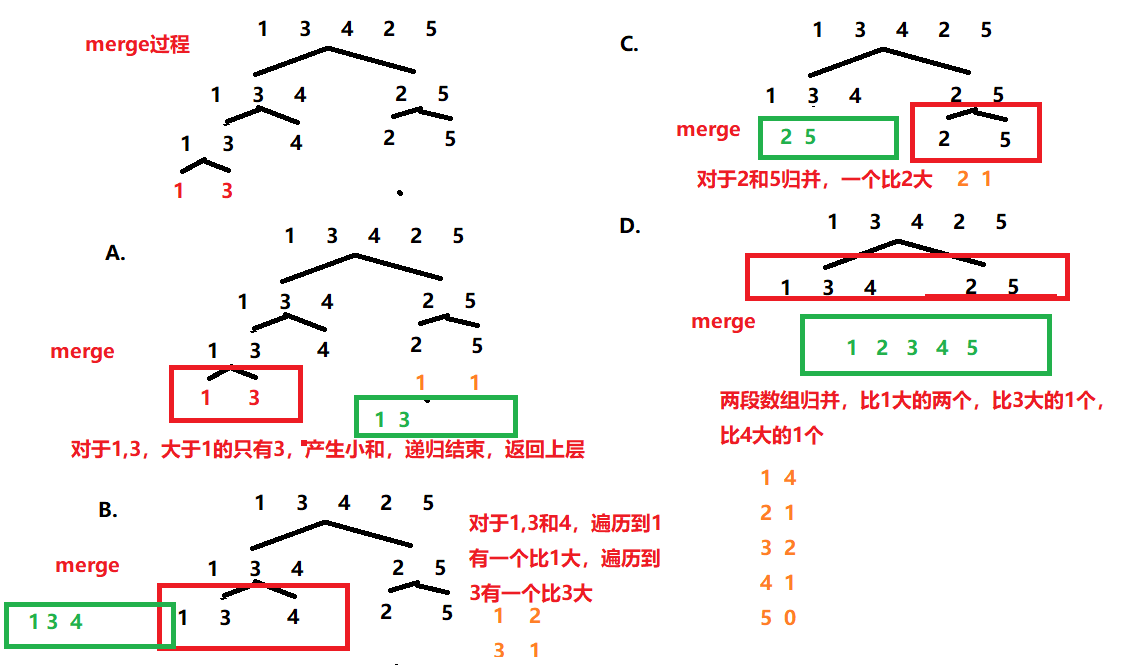
merge过程

  • A.根据递归树，对于1,3，大于1的只有3，产生小和，递归结束，返回上层 [1 1]
  • B.对于1,3,4，遍历到1有两个比1大；遍历到3有一个比3大 [1 2; 3 1]
  • C.对于递归右部分2,5，一个比2大 [2 1]
  • D.返回上层递归，两端数组归并，对于右半部分，比1大的有两个，比3大的有一个，比4大的有一个 [1 4; 2 1; 3 2; 4 1; 5 0]

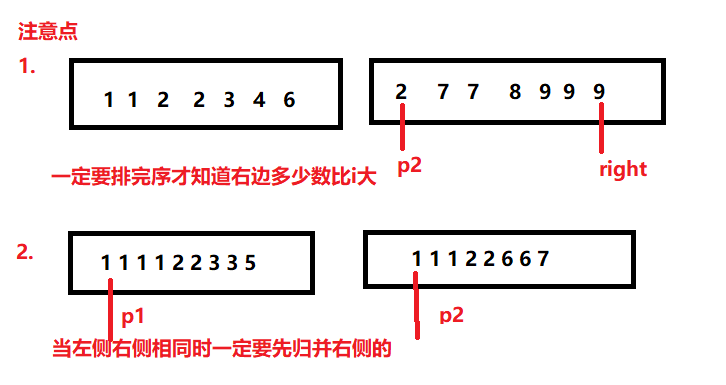
注意点

  • 一定要排完序才能直到右边多少数比i大
  • 当左右两侧相同时一定要先归并右侧的

merge

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public int merge(int[] arr, int left, int mid, int right) {
    int[] temp = new int[right - left + 1];
    int i = 0;
    // p1代表左侧第一个
    int p1 = left;
    // p2代表右侧第一个
    int p2 = mid + 1;
    int res = 0;
    while (p1 <= mid && p2 <= right) {
        //求小和
        res += arr[p1] < arr[p2] ? (right - p2 + 1) * arr[p1] : 0;
        //归并
        temp[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
    }
    //当左边元素有剩余
    while (p1 <= mid) {
        temp[i++] = arr[p1++];
    }
    //当右边元素有剩余
    while (p2 <= right) {
        temp[i++] = arr[p2++];
    }
    //重新拷贝回原始数组对应位置
    for (int j = 0; j < temp.length ; j++) {
        arr[left + j] = temp[j];
    }
    return res;
}

mergeSort

1
2
3
4
5
6
7
8
9
public int mergeSort(int[] arr, int left, int right) {
    if (left == right) {
        return 0;
    }
    int mid = left + ((right - left) >> 1);
    return mergeSort(arr, left, mid)
            + mergeSort(arr, mid + 1, right)
            + merge(arr, left, mid, right);
}

smallSum

1
2
3
4
5
6
public int smallSum(int[] arr) {
    if (arr == null || arr.length < 2) {
        return 0;
    }
    return mergeSort(arr, 0, arr.length - 1);
}

归并排序应用2—逆序对问题

算法思想：

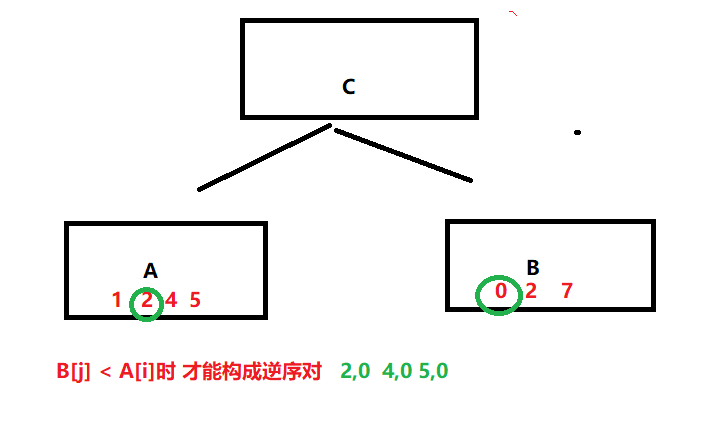
  • 把要统计逆序对个数的序列$C$沿着中间位置分成两个子序列A和B，递归计算子序列$A$和$B$中的逆序对个数，然后合并两个子序列，合并的同时计算所有$(a_i,a_j)$的数对中的逆序对的个数（$a_i$在子序列$A$，$a_j$在子序列$B$）
  • 由于子序列$A$和$B$是已经排好序的，在把$A$和$B$合并到$C$时，按照归并排序的合并过程，每次都选两个子序列中最小的元素加入到$C$中
  • 每次$A$中元素$a_i$被加入到$C$中，不会遇到新的逆序，因为$a_i$小于子序列$B$中剩下的每个元素，并且$a_i$出现在$B$中元素的前面。
  • 但每次$B$中的元素$b_j$被加到$C$中，说明它比子序列$A$中剩下的元素都小，由于$B$中所有元素本来都排在$A$后面，所以$b_j$就与$A$中剩下的所有元素都构成逆序对，此时$A$中剩下的元素个数就是与$b_j$构成的逆序对的个数。

图解

伪代码
mergeAndCount(A, B)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
初始化count= 0，C = 空
while A和B都不为空
  令ai和bj分别为A和B中的首元素
  if ai <= bj
    把ai加入到输出表C中
    A = A - {ai}
  else
    把bj加入到输出表C中
    B = B - {bj}
    count += A中剩下的元素
  endIf
endWhile
if A 为空
  把B中剩下元素加入到C
else
  把A中剩下元素加入到C
endIf
return 合并结果C和逆序对个数count

sortAndCount (C)

1
2
3
4
5
6
7
8
9
if L只有1个元素
  没有逆序,c1 = c2 = c3 = 0
else
  把这个表C均分成两半，A和B
  (c1, A) = sortAndCount(A)
  (c2, B) = sortAndCount(B)
  (c3, C) = mergeAndCount(A, B)
endIf
return (c1 + c2 + c3, C)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
public int merge(int[] arr, int left, int mid, int right) {
    int[] temp = new int[right - left + 1];
    int i = left, j = mid + 1, k = 0, count = 0;

    while (i <= mid && j <= right) {
        // 从mid开始划分成两段数组进行归并并找出逆序对
        if (arr[i] <= arr[j]) {
            temp[k++] = arr[i++];
        } else { // 当B段小于A段的数时，便找到了逆序对
            // 当B段小于A段的数时，便找到了逆序对
            temp[k++] = arr[j++];
            // 此时逆序对数为A段剩余元素数量
            count += mid - i + 1;
        }
    }
    
    while (i <= mid) {
        temp[k++] = arr[i++];
    }
    
    while (j <= right) {
        temp[k++] = arr[j++];
    }
    
    for (i = 0; i < temp.length; i++) {
        arr[left + i] = temp[i];
    }
    
    return count;
}

public int mergeSort(int[] arr, int left, int right) {
    if (left == right) {
        return 0;
    }
    int mid = left + ((right - left) >> 1);
    return mergeSort(arr, left, mid) +
            mergeSort(arr, mid + 1, right) +
            merge(arr, left, mid, right);
}

// main
public int reverseSort(int[] arr) {
    if (arr == null || arr.length < 1) {
        return 0;
    }
    return mergeSort(arr,0,arr.length-1);
}

堆排序应用

已知一个几乎有序的数组，几乎有序是指，如果把数组排好序的话，每个元素的移动距离可以不超过K，并且K相对于数组来说比较小，请选择一个合适的排序算法针对该数组进行排序

算法思想

遍历前7个数字，放入小根堆，小根堆最小值放0位置上。首先弹出小根堆放入0位置，然后将7位置上的值放入小根堆，弹出小根堆堆顶放入1位置，然后将8位置上的值放入小根堆，…，快结束后将整个小根堆弹出一次放入数组即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public void sortedArrDistanceLessK(int[] arr, int k) {
    // 小根堆
    PriorityQueue<Integer> heap = new PriorityQueue<>();
    int index = 0;
    // 遍历数组放入小根堆
    for (; index < Math.min(arr.length, k); index++) {
        heap.add(arr[index]);
    }
    int i = 0;
    for (; index < arr.length; i++, index++) {
        // 加入根堆
        heap.add(arr[index]);
        // 弹出小根堆堆顶
        arr[i] = heap.poll();
    }
    // 快结束后，将整个小根堆放入数组
    while (!heap.isEmpty()) {
        arr[i++] = heap.poll();
    }
}

快速排序应用—荷兰旗问题

经典问题

给定一个数组 arr，和一个数 num，请把小于等于 num 的数放在数组的左边，大于 num 的 数放在数组的右边。要求额外空间复杂度 $O(1)$，时间复杂度 $O(N)$。

算法思想

  • $arr[i]≤num$，arr[i]和小于等于区域下一个数交换，区域右扩，i++
  • $arr[i]>num$，i++

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public void partition(int[] arr, int left, int right, int target) {
    // 声明小于等于的边界
    int lessAndEqualBoundary = left - 1;
    int i = 0;

    while (i < arr.length) {
        if (arr[i] <= target) { 
            // 如果arr[i] <= target。arr[i]和小于等于边界下一个数交换
            swap(arr, ++lessAndEqualBoundary, i++);
        } else {
            // 如果arr[i] > target，i++
            i++;
        }
    }
}

荷兰旗问题

给定一个数组 arr，和一个数 num，请把小于 num 的数放在数组的左边，等于 num 的数放在数组的中间，大于 num 的数放在数组的右边。要求额外空间复杂度 $O(1)$，时间复杂度 $O(N)$。

算法思想

i表示小于区域的右边界，k表示大于区域的左边界

  • $arr[index]<num$，arr[index]和小于区域i下一个数交换，i++，`index++``
  • $arr[index]=num$，$index++$
  • $arr[index]>num$，arr[index]和大于区域k前一个数交换，k--，index不变（这时候前一个数是刚交换过来的，没有经过检查，index位置不能动）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public int[] Netherlands(int[] arr, int left, int right, int target) {
    int i = left - 1; // i 表示小于区域的右边界
    int k = right + 1; // k 表示大于区域的左边界

    while (left < k) {
        if (arr[left] < target) {
            swap(arr, ++i, left++); // 如果当前数小于num，当前数和小于区域下一个数交换，小于区域右扩（++i），left++
        } else if (arr[left] > target) { // 如果当前数大于num，当前数和大于区域前一个数交换，大于区域左扩（--k），由于双方刚交换完毕，left位置的数是大于区域交换过来的，未经检查，不能动left
            swap(arr, --k, left);
        } else { // 如果当前数等于num，直接下一轮迭代，也就是left++
            left++;
        }
    }
    // target边界
    return new int[] {i + 1, k - 1}; // 返回等于区域的左右边界
}

二分法应用

应用1

在一个有序数组中，找某个数是否存在

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 应用1
public boolean binarySearch(int[] sortedArr, int num) {
    if (sortedArr == null || sortedArr.length == 0) {
        return false;
    }
    int left = 0;
    int right = sortedArr.length - 1;
    int mid = 0;
    
    while (left < right) {
        mid = left + ((right - left) >> 1);
        if (sortedArr[mid] == num) {
            return true;
        } else if (sortedArr[mid] > num) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return sortedArr[left] == num;
}

应用2

在一个有序数组中，找大于等于某个数最左侧的位置 [重要]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 应用2
public int nearestIndex(int[] arr, int value) {
    int left = 0;
    int right = arr.length - 1;
    int mid = 0;
    int index = -1;

    while (left <= right) {
        mid = left + ((right - left) >> 1);
        if (arr[mid] >= value) { // value落在左边
            index = mid;
            right = mid - 1;
        } else { // value落在右边
            left = mid + 1;
        }
    }
    return index;
}

应用3

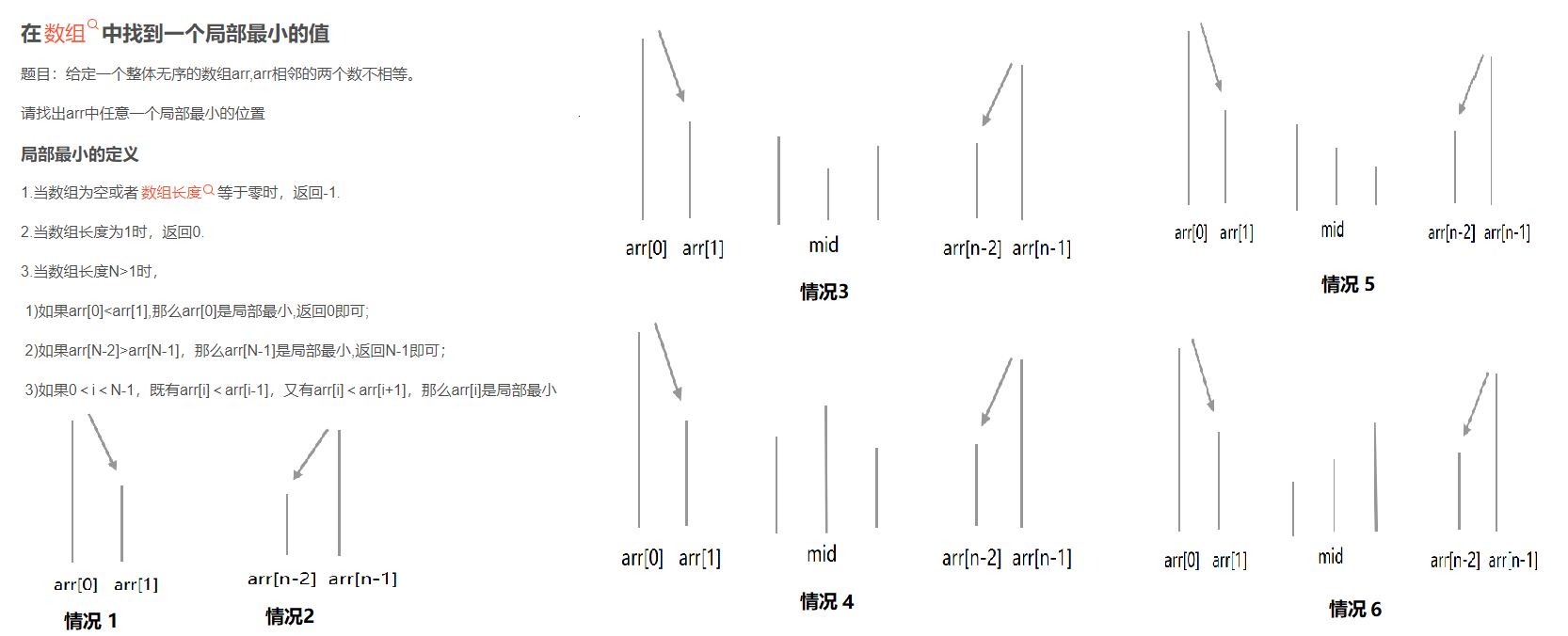
局部最小值问题

在 情况1 和 情况2 中由于情况1呈下降趋势，情况2呈上升趋势，所以arr数组一定有局部最小值

情况3
mid比它左边小，比它右边小，所以已经是局部最小，直接返回

情况4
mid比它左边大，也比它右边大。此时arr[0] ~ arr[1]是下降趋势, arr[mid-1]~arr[mid]是上升趋势，所以在此范围内数组arr一定存在局部最小。去掉mid右边的范围，直接找mid左边。

备注：虽然mid右边也存在局部最小，但是我们只需要返回一个局部最小，所以我们选择直接往mid左边找就可以了。

情况5
此时arr[mid] ~ arr[mid+1]是下降趋势, arr[n-2] ~ arr[n-1]是上升趋势,所以在此范围内数组arr一定存在局部最小。去掉mid左边的范围，找mid右边。

情况6
此时arr[0] ~ arr[1]是下降趋势， arr[mid-1] ~ arr[mid]是上升趋势，所以在此范围内数组arr一定存在局部最小。去掉mid右边的范围，找mid左边。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
// 应用3
public int LocalMin(int[] arr) {

    if (arr == null || arr.length == 0) {
        return -1;
    }

    int N = arr.length;
    if (N == 1) {
        return 0;
    }

    if (arr[0] < arr[1]) {
        return 0;
    }

    if (arr[N - 1] < arr[N - 2]) {
        return N - 1;
    }
    int left = 0;
    int right = N - 1;

    /**
     *  L...R 肯定有局部最小
     *  保证L~R之间至少有三个数，我们才能进行二分
     *  如果L~R之间不够三个数,我们直接比较L和R哪个更小，哪个就是局部最小
     */
    while (left < right - 1) {
        int mid = left + ((right - left) >> 1);
        if (arr[mid] < arr[mid - 1] && arr[mid] < arr[mid + 1]) {
            return mid;
        } else {
            // 1 left>mid  mid>right
            // 2 left<mid  mid<right
            // 3 left<mid  mid>right
            if (arr[mid] > arr[mid - 1]) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
    }
    // 循环结束之后,L>=R-1. 数组内要么是两个数，要么是一个数
    return arr[left] < arr[right] ? left : right;
}