数据结构-3-链表

引言：

方法论

• 对于笔试：一切为了时间复杂度，不用在乎空间复杂度
• 对于面试：时间复杂度放在首位，空间复杂度尽量最小

重要技巧

• 额外数据结构记录（哈希表等）
• 快慢指针

链表回文

方式1 利用快慢指针走到中点，将链表后一半放入栈

// 方式1
public boolean isPalindrome(Node head) {
if (head == null || head.next == null) {
    return true;
}
// 定义栈
Stack<Node> stack = new Stack<Node>();

// 定义右指针
Node right = head.next;
// 定义当前指针
Node cur = head;

while (cur.next != null || cur.next.next != null) {
    // 慢指针步长为1
    right = right.next;
    // 快指针步长为2
    cur = cur.next.next;
}

// 将链表的后半部分放入栈
while (right != null) {
    stack.push(right);
    right = right.next;
}

// 判断
while (!stack.isEmpty()) {
    if (head.val != stack.pop().val) {
        return false;
    }
    head = head.next;
}

return true;
}

方式2 利用快慢指针走到中点，将链表后一部分反转，双指针遍历

// 方式2
public boolean isPalindrome2(Node head) {
    if (head == null || head.next == null) {
        return true;
    }

    // 定义慢指针n1
    Node slowNode = head;
    // 定义快指针n2
    Node fastNode = head;

    /*
        当整个循环结束后慢指针s位于中点，快指针f位于null
              S
        1->2->3->4->5->null
                        f

        */

    // 当快指针走到链表末尾，慢指针便到达链表中点
    while (fastNode.next != null && fastNode.next.next != null) {
        // 慢指针步长为1
        slowNode = slowNode.next;
        // 快指针步长为2
        fastNode = fastNode.next.next;
    }

    // 快指针此时指向慢指针右半部分的第一个节点
    fastNode = slowNode.next;
    // 中间节点的后继断链
    slowNode.next = null;
    // 定义辅助节点n3
    Node tempNode = null; 

    /*
        快指针此时指向慢指针右半部分的第一个节点,中间节点的后继断链
              S
        1->2->3  4->5
                 f

        */
    // 链表右半部分转置
    while (fastNode != null) {
        // n3保存后继节点
        tempNode = fastNode.next;
        // 开始转置
        fastNode.next = slowNode;
        slowNode = fastNode;
        fastNode = tempNode;
    }
    // n3指向转置后的链表的（从左至右）最后一个结点
    tempNode = slowNode;
    // n2指向转置后的链表的（从左至右）第一个结点
    fastNode = head;
    boolean res = true;

    // 回文判断
    while (slowNode != null && fastNode != null) {
        if (slowNode.val != fastNode.val) {
            res = false;
            break;
        }
        // 从右到左
        slowNode = slowNode.next;
        // 从左到右
        fastNode = fastNode.next;
    }

    slowNode = tempNode.next;
    tempNode.next = null;

    // 复原链表
    while (slowNode != null) {
        fastNode = slowNode.next;
        slowNode.next = tempNode;
        tempNode = slowNode;
        slowNode = fastNode;
    }
    return res;
}

链表划分

问题

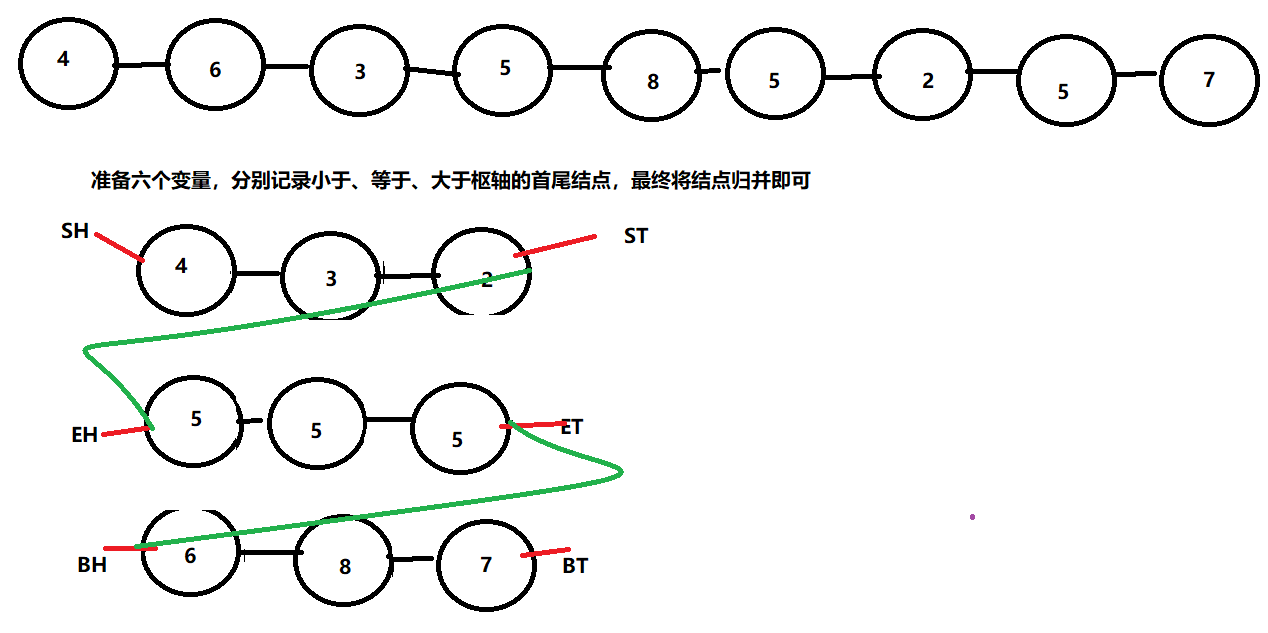
给定一个单链表的头节点head，节点的值类型是整型，再给定一个整数pivot。实现一个调整链表的函数，将链表调整为左部分都是值小于pivot的节点，中间部分都是值等于pivot的节点，右部分都是值大于pivot的节点。

进阶

• 在实现原问题功能的基础上增加如下的要求

• 调整后所有小于pivot的节点之间的相对顺序和调整前一样

• 调整后所有等于pivot的节点之间的相对顺序和调整前一样
• 调整后所有大于pivot的节点之间的相对顺序和调整前一样
• 时间复杂度请达到 $O(N)$，额外空间复杂度请达到$O(1)$。

算法图解

public Node listPartition(Node head, int pivot) {
    // 定义sH、sT（小于pivot的部分）
    Node sH = null; Node sT = null;
    // 定义eH、eT（等于pivot的部分）
    Node eH = null; Node eT = null;
    // 定义bH、bT（大于pivot的部分）
    Node bH = null; Node bT = null;
    Node next = null;

    while (head != null) {
        // 断链
        next = head.next;
        head.next = null;

        // 若当前值小于枢轴
        if (head.val < pivot) {
            // 若左半部分没有任何节点时
            // s头指针sH和s尾指针sT都指向head
            if (sH == null) {
                sH = head;
                sT = head;
            } else { // 否则
                // s尾指针sT连接当前节点
                sT.next = head;
                // 更新s尾指针sT
                sT = head;
            }
        } else if (head.val == pivot) { // 若当前值等于枢轴
            // 若中间部分没有任何节点时
            // e头指针eH和e尾指针eT都指向head
            if (eH == null) {
                eH = head;
                eT = head;
            } else {
                // e尾指针eT连接当前节点
                eT.next = head;
                // 更新e尾指针eT
                eT = head;
            }

        } else { // 若当前值大于枢轴
            // 如果右半部分没有任何结点时
            // b头指针bH和b尾指针bT都指向head
            if (bH == null) {
                bH = head;
                bT = head;
            } else {
                // b尾指针bT连接当前节点
                bT.next = head;
                // 更新b尾指针bT
                bT = head;
            }
        }

        // 更新当前节点位置
        head = next;
    }

    // 如果存在左半段链表[见图解]  （连接左半部分链表）
    if (sT != null) {
        // s尾指针sT后继指向e头指针eH
        sT.next = eH;
        eT = eT == null ? sT : eT;
    }

    // 如果左半段链表和中间段链表不是都没有[见图解] （在上代码基础上如果存在连接好的或者无需连接的左半部分，则连接右半部分）
    if (eT != null){
        eT.next = bH;
    }
    
    /**
     * 如果左半部分头指针存在，返回sH
     * 如果左半部分头指针不存在，判断中间部分头指针是否存在
     * 如果中间部分头指针存在，返回eH
     * 如果中间部分头指针不存在，返回右半部分的头指针bH
     */
    return sH != null ? sH : eH != null ? eH : bH;
}

复制含有随机指针节点的链表

问题

定义一种特殊单链表结点类，描述如下:

class Node {
	int value;
	Node next;
	Node rand;
	Node(int val) {
		value = val;
	}
}

rand指针是单链表结点结构中新增的指针，rand可能指向链表中的任意一个结点，也可能指向null。给定一个由Node结点类型组成的无环单链表的头结点head，请实现一个函数完成这个链表的复制，并返回复制的新链表的头结点。
[要求] 时间复杂度$O(N)$，额外空间复杂度 $O(1)$

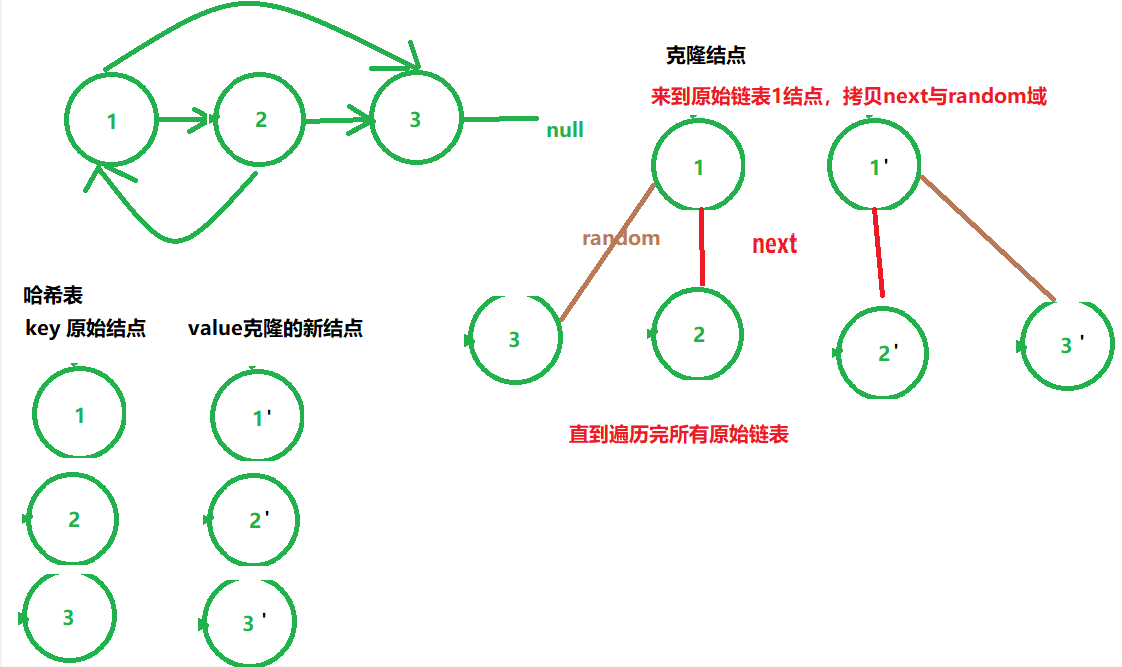
算法思想

准备哈希表，键值对为原始节点,克隆的新节点，克隆操作是，来到原始链表节点1，拷贝next与random，直到遍历完所有原始链表

public Node copyListWithRandom(Node head) {
    // 构建原始节点映射至克隆节点的哈希表
    HashMap<Node, Node> map = new HashMap<>();
    Node cur = head;

    // 拷贝原始节点
    while (cur != null) {
        // <原始节点，原始节点对应的拷贝节点>
        map.put(cur, new Node(cur.value));
        cur = cur.next;
    }

    cur = head;

    while (cur != null) {
        // 拷贝节点的next域指向原始节点的next域对应的拷贝节点
        map.get(cur).next = map.get(cur.next);
        // 拷贝节点的rand域指向原始节点rand域对应的拷贝节点
        map.get(cur).rand = map.get(cur.rand);
        cur = cur.next;
    }
    
    return map.get(head);
}

链表相交问题

问题

给定两个可能有环也可能无环的单链表，头结点head1和head2。请实现一个函数，如果两个链表相交，请返回相交的第一个结点。如果不相交，返回null。

要求

如果两个链表长度和为 $N$，时间复杂度达到 $O(N)$，额外空间复杂度达到 $O(1)$

单链表是否有环

问题

如何判断一个链表有环，如果有，返回第一个入环口，没有返回null

算法思想

• 设置快慢指针，快指针走两步，慢指针走一步

• 如果没有环快指针会先到达终点

• 如果有环，快指针与慢指针会在环中某一位置相遇

• 当快慢指针相遇时，快指针指向head，与慢指针同步移动，会在第一个入环口相遇。

// 单链表是否有环
public Node getLoopNode(Node head) {
    // 违规条件
    if (head == null || head.next == null) {
        return null;
    }

    // 慢指针
    Node slow = head.next;
    // 快指针
    Node fast  = head.next.next;

    // 慢指针和快指针同步移动
    while (fast != slow) {
        if (fast.next == null || fast.next.next == null) {
            return null;
        }
        fast = fast.next.next;
        slow = slow.next;
    }

    // 当快慢指针相遇时
    fast = head;

    // fast与slow同步移动
    while (fast != slow) {
        fast = fast.next;
        slow = slow.next;
    }

    return slow;
}

备注：如果一个链表有环，另一个链表无环，那么这个链表是无论也不可能相交的。能相交的就是两个情况：

• 两个链表都无环

• 两个链表都有环

  两个无环链表相交

  问题

如何判断两个无环链表是否相交，相交则返回第一个相交节点，不相交返回null

算法思想

• 指针1从头结点开始，走到最后一个结点（不是结束），统计链表1的长度len1，记录链表1的最后一个结点为end1

• 链表2从头结点开始，走到最后一个结点（不是结束），统计链表2的长度len2，记录链表2的最后给一个结点end2

• 如果end1!=end2，说明两个链表不相交，返回null即可；如果end1==end2，说明两个链表相交，进入下一步. 来寻找第一个相交的结点

• 如果链表1比较长，链表1就先走len1-len2步；如果链表2比较长，链表2就先走len2-len1步。然后两个链表一起走，两个链表第一次走到一起的结点就是第一个相交的结点

// 两个无环链表相交
public Node noLoop(Node head1, Node head2) {
    // 违规条件
    if (head1 == null || head2 == null) {
        return null;
    }
    // cur1
    Node cur1 = head1;
    // cur2
    Node cur2 = head2;
    // len
    int len = 0;

    // len1
    while (cur1.next != null) {
        len++;
        cur1 = cur1.next;
    }

    // len2
    while (cur2.next != null) {
        len--;
        cur2 = cur2.next;
    }

    // 判断
    if (cur1 != cur2) {
        return null;
    }

    // cur1选择长的链表
    cur1 = len > 0 ? head1 : head2;

    // cur2选择短的链表
    cur2 = cur1 == head1 ? head2 : head1;

    // len
    len = Math.abs(len);

    // 移动cur1便于下一步同步移动
    while (len != 0) {
        len--;
        cur1 = cur1.next;
    }

    // 两个指针同步移动
    while (cur1 != cur2) {
        cur1 = cur1.next;
        cur2 = cur2.next;
    }
    return cur1;
}

两个有环链表相交

问题

如何判断两个有环链表相交，相交则返回第一个相交节点，不相交返回null

[loop1 == loop2 两个链表相交图示]

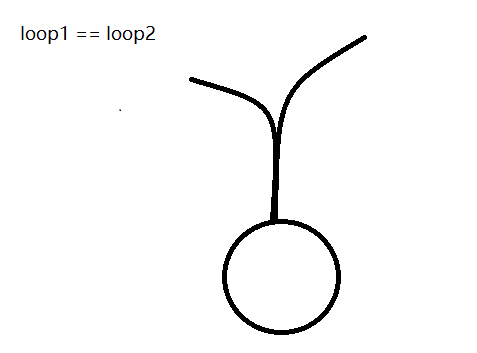
[loop1 != loop2 两个链表不相交图示]

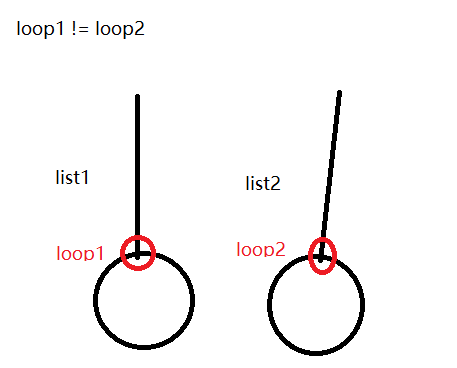
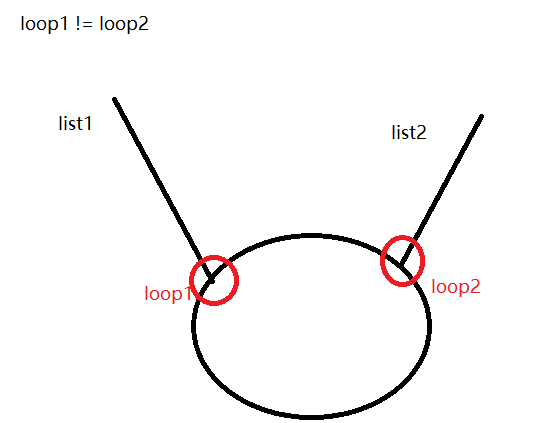
[loop1 != loop2两个链表相交图示]

算法思想

• 让链表1从入环扣1（loop1）出发（由于loop1和之后的所有结点都在环上，将来一定能返回loop1）

• 如果回到loop1之前没有遇到loop2，说明两个链表结构如图[loop1 != loop2 两个链表不相交图示]，即不相交，返回null

• 如果回到loop1之前遇到loop2，说明两个链表结构如图[loop1 != loop2两个链表相交图示]，也就是相交

• 由于loop1和loop2都在两条链表上，只不过loop1是离链表1较近的结点，loop2是离链表2较近的结点，返回两者中任意一个即可

// 两条有环链表相交
public Node bothLoop(Node head1, Node head2, Node loop1, Node loop2){
    // 定义两个哨兵
    Node cur1 = null;
    Node cur2 = null;

    // 图示1情况
    if (loop1 == loop2) {
        cur1 = head1;
        cur2 = head2;
        int len = 0;
        while (cur1 != loop1) {
            len++;
            cur1 = cur1.next;
        }
        while (cur2 != loop2) {
            len--;
            cur2 = cur1.next;
        }
        cur1 = len > 0 ? head1 : head2;
        cur2 = cur1 == head1 ? head2 : head1;
        len = Math.abs(len);
        while (len != 0) {
            len--;
            cur1 = cur1.next;
        }
        while (cur1 != cur2) {
            cur1 = cur1.next;
            cur2 = cur2.next;
        }
        return cur1;
    } else { // 图示2和3
        cur1 = loop1.next;
        while (cur1 != loop1) {
            if (cur1 == loop2) { // 图3
                return loop1;
            }
            cur1 = cur1.next;
        }
        return null;
    }
}

Total

// main
public Node getIntersectNode(Node head1, Node head2) {
    
    // 违规条件
    if (head1 == null || head2 == null) {
        return null;
    }
    
    // 判断第一个链表有没有环
    Node loop1 = getLoopNode(head1);
    
    // 判断第一个链表有没有环
    Node loop2 = getLoopNode(head2);
    
    // 情况1
    if (loop1 == null && loop2 == null) {
        return noLoop(head1, head2);
    }
    
    // 情况2/3
    if (loop1 != null && loop2 != null) {
        return bothLoop(head1, loop1, head2, loop2);
    }
    
    return null;
}