掌握情况
| 题目 |
通关 |
| 反转字符串 |
通过 |
| 反转字符串Ⅱ |
通过 |
| 替换空格 |
通过 |
| 左旋转字符串 |
通过 |
| 实现 strStr() |
未通过 |
| 重复的子字符串 |
未通过 |
反转字符串
LeetCode 344.反转字符串
问题
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 s 的形式给出。
不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
双指针
1
2
3
4
5
6
7
8
| public void reverseString(char[] s) {
int n = s.length;
for (int left = 0, right = n - 1; left < right; ++left, --right) {
char tmp = s[left];
s[left] = s[right];
s[right] = tmp;
}
}
|
反转字符串 Ⅱ
LeetCode 541.反转字符串 II
问题
给定一个字符串 s 和一个整数 k,从字符串开头算起,每计数至 2k 个字符,就反转这 2k 字符中的前 k 个字符。
- 如果剩余字符少于
k 个,则将剩余字符全部反转。
- 如果剩余字符小于
2k 但大于或等于 k 个,则反转前 k 个字符,其余字符保持原样。
算法思想
反转每个下标从 $2k$ 的倍数开始的,长度为 $k$ 的子串。若该子串长度不足 $k$ ,则反转整个子串。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public String reverseStr(String s, int k) {
int n = s.length();
char[] arr = s.toCharArray();
for (int i = 0; i < n; i += 2 * k) {
reverse(arr, i, Math.min(i + k, n) - 1);
}
return new String(arr);
}
public void reverse(char[] arr, int left, int right) {
while (left < right) {
char temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
left++;
right--;
}
}
|
替换空格
LCR 122. 路径加密
问题
假定一段路径记作字符串 path,其中以 “.“ 作为分隔符。现需将路径加密,加密方法为将 path 中的分隔符替换为空格 “ “,请返回加密后的字符串。
1
2
3
4
5
6
7
8
9
| public String pathEncryption(String path) {
char[] ch = path.toCharArray();
for (int i = 0; i < ch.length; i++) {
if (ch[i] == '.') {
ch[i] = ' ';
}
}
return new String(ch);
}
|
左旋转字符串
LCR 182. 动态口令
问题
某公司门禁密码使用动态口令技术。初始密码为字符串 password,密码更新均遵循以下步骤:
- 设定一个正整数目标值
target
- 将
password 前 target 个字符按原顺序移动至字符串末尾
请返回更新后的密码字符串。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public String dynamicPassword(String password, int target) {
char[] ch = password.toCharArray();
int len = ch.length - 1;
reverse(ch, 0, target - 1);
reverse(ch, target, len);
reverse(ch, 0, len);
return new String(ch);
}
public void reverse(char[] str, int begin, int end) {
for(int i = begin, j = end; i < j; i++, j--) {
char temp = str[i];
str[i] = str[j];
str[j] = temp;
}
}
|
KMP
28. 找出字符串中第一个匹配项的下标
问题
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。
KMP
参考文章 KMP
三叶大佬的题解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| public int[] getNext(char[] pattern) {
if (pattern.length == 1) {
return new int[]{-1};
}
int[] next = new int[pattern.length];
next[0] = -1;
next[1] = 0;
int i = 2, j = 0;
while (i < next.length) {
if (pattern[i - 1] == pattern[j]) {
next[i++] = ++j;
} else if (j > 0) {
j = next[j];
} else {
next[i++] = 0;
}
}
return next;
}
public int strStr(String str, String pattern) {
if (str == null || pattern == null ||
pattern.length() < 1 || str.length() < pattern.length()) {
return -1;
}
char[] mainStr = str.toCharArray();
char[] subStr = pattern.toCharArray();
int i = 0, j = 0;
int[] next = getNext(subStr);
while (i < mainStr.length && j < subStr.length) {
if (mainStr[i] == subStr[j]) {
i++;
j++;
} else if (next[j] == -1) {
i++;
} else {
j = next[j];
}
}
return j == subStr.length ? i - j : -1;
}
|
暴力法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public int nativeSolution(String str, String pattern) {
int n = str.length(), m = pattern.length();
char[] s_char = str.toCharArray(), p_char = pattern.toCharArray();
for (int i = 0; i <= n - m; i++) {
int index = i, begin = 0;
while (begin < m && s_char[index] == p_char[begin]) {
index++;
begin++;
}
if (begin == m) {
return i;
}
}
return -1;
}
|
思考题

重复的子字符串
459. 重复的子字符串
问题
给定一个非空的字符串 s ,检查是否可以通过由它的一个子串重复多次构成。
示例
1
2
3
4
5
6
7
8
9
10
| 示例 1:
输入: s = "abab"
输出: true
解释: 可由子串 "ab" 重复两次构成。
示例 2:
输入: s = "aba"
输出: false
|
枚举
算法思想
如果一个长度为 n 的字符串 s 可以由它的一个长度为 n' 的子串 s' 重复多次构成,那么:
可以从小到大枚举 n′,并对字符串 s 进行遍历,进行上述的判断。 注意到一个小优化是,因为子串至少需要重复一次,所以 n' 不会大于 n 的一半,只需要在$[1, \frac{n}{2}]$ 的范围内枚举 n' 即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public boolean repeatedSubstringPattern(String s) {
int n = s.length();
for (int i = 1; i * 2 <= n; i++) {
if (n % i == 0) {
boolean match = true;
for (int j = i; j < n; j++) {
if (s.charAt(j) != s.charAt(j - i)) {
match = false;
break;
}
}
if (match) {
return true;
}
}
}
return false;
}
|
移动匹配
算法思想
当一个字符串 s:abcabc,内部由重复的子串组成,那么这个字符串的结构一定是这样的:

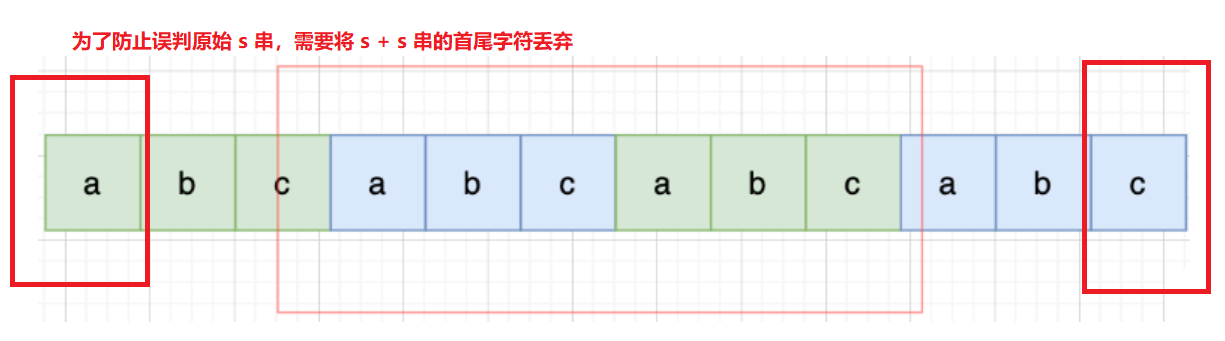
那么既然前面有相同的子串,后面有相同的子串,用 s + s,这样组成的字符串中,后面的子串做前串,前面的子串做后串,就一定还能组成一个 s,如图:

所以判断字符串 s 是否由重复子串组成,只要两个 s 拼接在一起,里面还出现一个 s,就说明是由重复子串组成。 当然,我们在判断 s + s 拼接的字符串里是否出现一个 s 的的时候,要刨除 s + s 的首字符和尾字符,这样避免在 s + s 中搜索出原来的s,我们要搜索的是中间拼接出来的 s 。
1
2
3
| public boolean repeatedSubstringPattern(String s) {
return (s + s).indexOf(s, 1) != s.length();
}
|
KMP
参考答案
结论
下一段复习理解 KMP,再去完成该题













