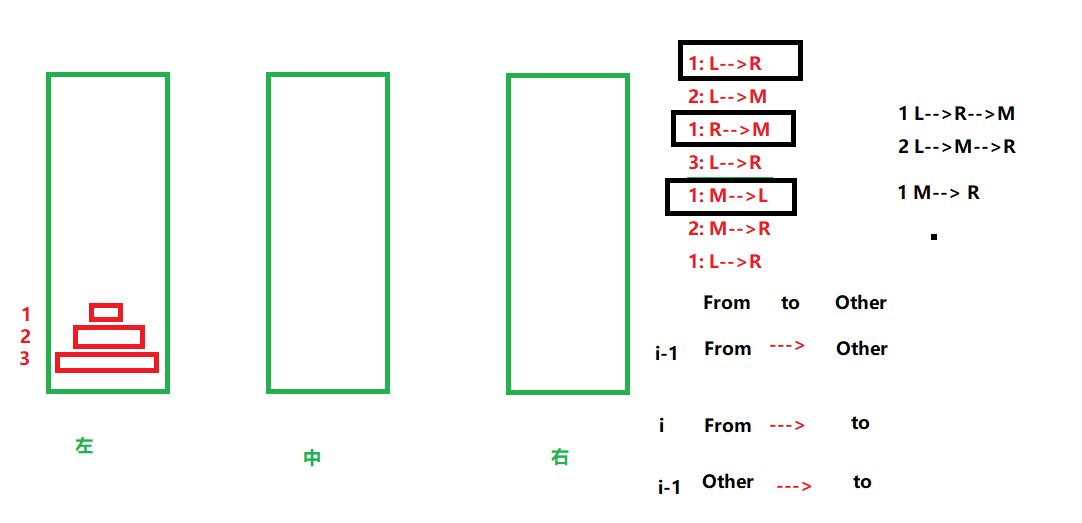
Hanoi
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public void process(int index, String from, String to, String other) {
if (index == 1) {
System.out.println("将" + index + "从" + from + "移动到" + to);
} else {
process(index - 1, from, other, to);
System.out.println("将" + index + "从" + from + "移动到" + to);
process(index - 1, other, to, from);
}
}
public void hanoi(int n) {
if (n > 0) {
process(n, "左", "右", "中");
}
}
|
打印一个字符串的全部子序列,包括空串

算法思想
对于来到的第i位置,我们有两种选择
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| public void process(char[] chs, int index) {
if (index == chs.length) {
System.out.println(String.valueOf(chs));
return;
}
process(chs, index + 1);
char temp = chs[index];
chs[index] = 0;
process(chs, index + 1);
chs[index] = temp;
}
public void printAllSubSquences(String str) {
char[] chs = str.toCharArray();
process(chs, 0);
}
|
使用递归函数逆序栈(不能申请额外空间)
只能利用栈操作和递归逆序栈,栈一次仅能对一个元素操作,所以只能从弹出栈底出发,然后压栈操作
递归函数1:将栈stack的栈底元素返回并移除
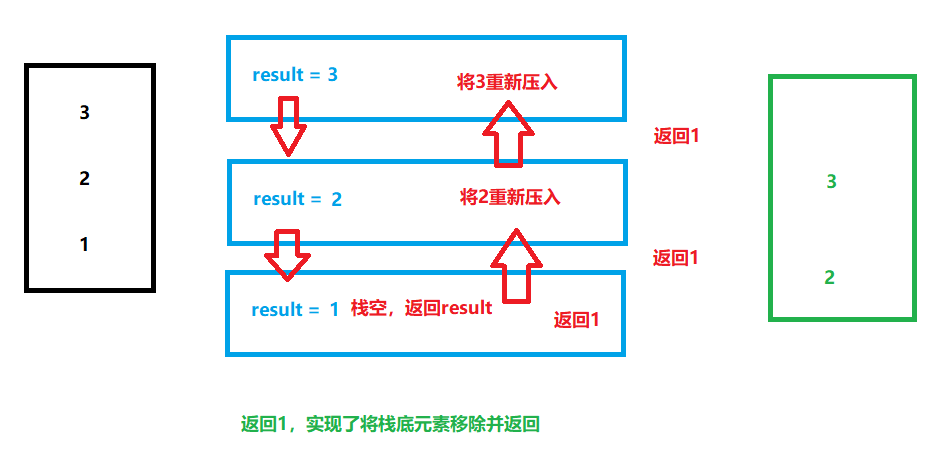
递归函数2:逆序一个栈
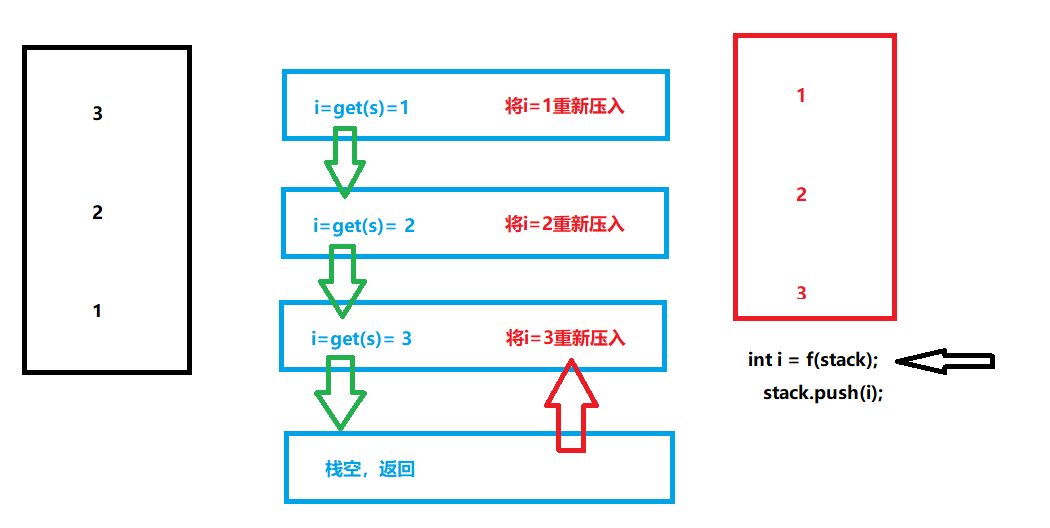
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
public int getAndRemoveLastElement(Stack<Integer> stack) {
int result = stack.pop();
if (stack.isEmpty()) {
return result;
} else {
int last = getAndRemoveLastElement(stack);
stack.push(result);
return last;
}
}
public void reverse(Stack<Integer> stack) {
if (stack.isEmpty()) {
return;
} else {
int i = getAndRemoveLastElement(stack);
reverse(stack);
stack.push(i);
}
}
|
数字字符串转字母组合的种数
规定1和A对应、2和B对应、3和C对应… 那么一个数字字符串比如”111”,就可以转化为AAA、KA和AK。 给定一个只有数字字符组成的字符串str,返回有多少种转化结果。
算法思想
定义递归函数process(i),其含义是str[0...i-1]是已经选择好的情况,str[i..N]是没有转换完的情况,最后返回合法答案
情况1 p(n)表示当前来到尾部,答案已经转换完成,只有一种结果
情况2 不满足情况1且str[i]='0',说明是 以’0’开头的违规情况 ,返回0种结果
情况3 当前i是以1开头,两种情况,其一是以str[i]构成一位数的答案,其二是以str[i]和str[i+1]构成两位数的答
情况4 当前i是以2开头,两种情况,其一是以str[i]构成一位数的答案,其二是在以str[i]和str[i+1]构成两位数 不超过26 情况下构成另一种答案
情况5 剩余的情况是 以3-9开头 只有一种答案
综上相加即为返回结果
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
public int process(char[] str, int i) {
if (i == str.length) {
return 1;
}
if (str[i] == '0') {
return 0;
}
if (str[i] == '1') {
int res = process(str, i + 1);
if (i + 1 < str.length) {
res += process(str, i + 2);
}
return res;
}
if (str[i] == '2') {
int res = process(str, i + 1);
if (i + 1 < str.length && (str[i + 1] >= '0' && str[i + 1] <= '6')) {
res += process(str, i + 2);
}
return res;
}
return process(str, i + 1);
}
|
背包问题
给定两个长度都为 $N$ 的数组weights 和 values,weights[i] 和 values[i] 分别代表 i 号物品的 重量 和 价值 。给定一个正数bag,表示一个 载重 bag的袋子,你装的物品不能超过这个重量。返回你能装下最多的价值是多少?
算法思想
从左到右的尝试模型,来到i位置做出选择,或者不做出选择,最终合并答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
public int process(int[] weights, int[] values, int i, int alreadyweight, int bag) {
if (alreadyweight > bag) {
return 0;
}
if (i == weights.length) {
return 0;
}
return Math.max(
values[i] + process(weights, values, i + 1, alreadyweight + weights[i], bag),
process(weights, values, i + 1, alreadyweight, bag));
}
|
纸牌博弈
给定一个整型数组arr,代表数值不同的纸牌排成一条线。玩家A和玩家B依次拿走每张纸牌,规定玩家A先拿,玩家B后拿,但是每个玩家每次只能拿走 最左或最右 的纸牌,玩家A和玩家B都 绝顶聪明。请返回最后获胜者的分数。
arr = [1, 2, 100, 4]
开始时,玩家A只能拿走1 或 4。如果开始时玩家A拿走 1,则排列变为 [2,100,4] ,接下来玩家B可以拿走 2 或 4,然后继续轮到玩家A
如果开始时玩家A拿走 4,则排列变为 [1,2,100],接下来玩家B可以拿走 1 或 100,然后继续轮到玩家A…
玩家A作为绝顶聪明的人不会先拿 4,因为拿 4 之后,玩家B将拿走 100。所以玩家A会先拿 1,让排列变为 [2,100,4],接下来玩家B不管怎么选,100 都会被玩家A拿走。玩家A会获胜,分数为101 。所以返回101
arr = [1, 100, 2]
开始时,玩家A不管拿 1还是 2,玩家B作为绝顶聪明的人,都会把 100拿走。玩家B会获胜,分数为100。所以返回 100
先手玩家
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
public int first(int[] arr, int i, int j) {
if (i == j) {
return arr[i];
}
return Math.max(
arr[i] + second(arr, i + 1, j),
arr[j] + second(arr, i, j - 1)
);
}
|
后手玩家
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
public int second(int[] arr, int i, int j) {
if (i == j) {
return 0;
}
return Math.min(
first(arr, i + 1, j),
first(arr, i, j - 1)
);
}
|
最终赢家
1
2
3
4
5
6
| public int win(int[] arr) {
if(arr == null || arr.length == 0) {
return 0;
}
return Math.max(first(arr, 0, arr.length - 1), second(arr, 0, arr.length - 1));
}
|
N 皇后
N皇后问题是指在 N×N 的棋盘上要摆 N个皇后,要求任何两个皇后 不同行、不同列,也不在同一条斜线上 。给定一个整数n,返回皇后的摆法有多少种。
测试用例
- n=1,返回1
- n=2或3,2皇后和3皇后问题无论怎么摆都不行,返回0
- n=8,返回92
暴力递归
算法思想
从第 i 行开始摆放皇后,在 $(i,j)$ 位置放置了一个皇后,接下来
整个第 i 行位置不能放皇后
整个第 j 列位置不能放皇后
如果位置 $(a,b)$ 满足 $∣a−i∣==∣b−j∣$ ,说明两点共斜线,不能放置皇后
判断摆放位置是否合法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
public boolean isValid(int[] record, int i, int j) {
for(int k = 0; k < i; k++) {
if(j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {
return false;
}
}
return true;
}
|
暴力递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
public int process(int i, int[] record, int n) {
if (i == n) {
return 1;
}
int res = 0;
for (int j = 0; j < n; j++) {
if(isValid(record, i, j)) {
record[i] = j;
res += process(i + 1, record, n);
}
}
return res;
}
|
调用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public int NQueens(int n) {
if (n < 1) {
return 0;
}
int[] record = new int[n];
return process(0, record, n);
}
|
位运算(局限性)
局限性
当前由于int位限制,仅支持到32皇后以内的摆法



1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
public int process(int limit, int colLim, int leftDiaLim,
int rightDiaLim) {
if (colLim == limit) {
return 1;
}
int pos = 0;
int mostRightOne = 0;
pos = limit & (~(colLim | leftDiaLim | rightDiaLim));
int res = 0;
while (pos != 0) {
mostRightOne = pos & (~pos + 1);
pos = pos - mostRightOne;
res += process(limit, colLim | mostRightOne,
(leftDiaLim | mostRightOne) << 1,
(rightDiaLim | mostRightOne) >>> 1);
}
return res;
}
|
1
2
3
4
5
6
7
8
9
10
| public int NQueens(int n) {
if (n < 1 || n > 32) {
return 0;
}
int limit = n == 32 ? -1 : (1 << n) - 1;
return process(limit, 0, 0, 0);
}
|
















