引入问题

给定两个字符串str和match，长度为 $N$ 和 $M$ 。如果字符串str中含有子串match，返回match在str中开始位置。

如果match的长度大于str长度（ $M>N$ ），str必然不会含有match，可直接返回-1。但如果 $N≥M$ ，要求算法复杂度为 $O(M)$

next数组

next数组含义

next[i] 的含义是在 match[i] 之前的字符串 match[0..i-1] 中，必须以 match[i-1] 结尾的 后缀子串 与必须以match[0]开头的 前缀子串 最大匹配长度

  • 后缀字符不能包含match[0]，即整个后缀不能是本身

  • 前缀字符不能包含match[i-1]，即整个前缀不能是本身

求解next数组

match[0] ：他之前没有字符，next[0] 规定为 -1

match[1] ：next数组定义要求任何子串后缀不能包含第一个字符，故 match[1] 之前的字符串只有长度为0的后缀字符串，next[1] 规定为0

match[i]

1.从左至右依次求解next，求解 next[i] 时，next[i-1] 已经求出，如图I区域是最长匹配前缀，k区域是最长匹配后缀

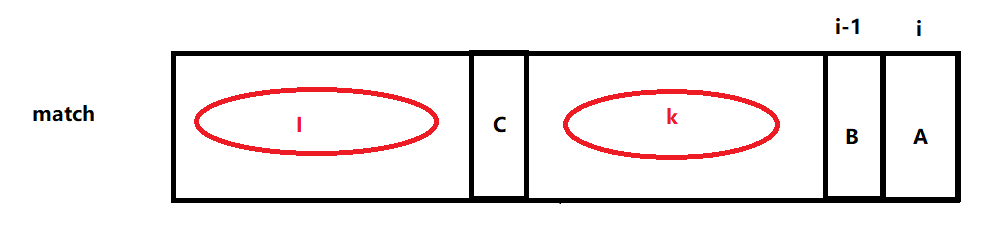
2.如果C和B相等，A之前最长公共前后缀就可以确定，前缀子串为I区域+C，后缀子串为k区域+B，即 next[i]=next[i-1]+1

3.如果C和B不相等，就要看C之前的前缀和后缀匹配情况

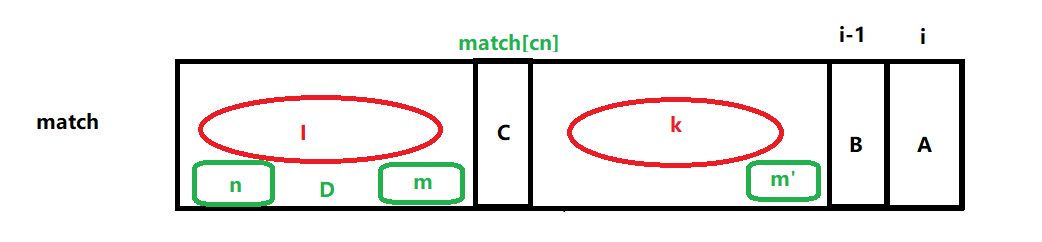
假设字符C是第cn个字符，那么next[cn]就是其最长前缀和最长后缀的匹配长度

m、n区域是相等的，m'区域为k区域最右的区域且长度与m区域相等，字符D是n区域后面一个字符，

所以接下来比较字符D和字符B是否相等

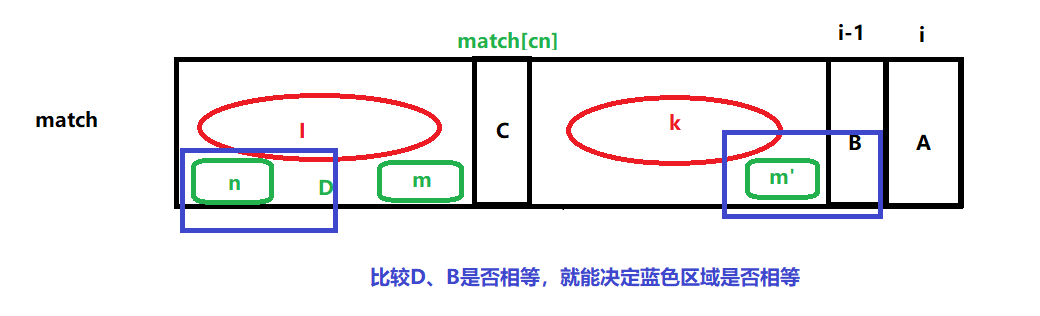
  • 如果B、D相等，A字符之前的最长前缀与后缀匹配区域就可以确定，前缀区域为n区域+D，后缀区域是m'区域+B，则令next[i]=next[cn]+1

  • 如果B、D不等，继续往前跳到D字符，每一步都有新的字符和B比较，只要相等的情况，next[i] 就确定

4.如果跳到最左位置(match[0]位置)，此时next[0]=-1，说明字符A之前的字符串不存在前缀和后缀的匹配情况，则next[i]=0

KMP算法

假设从str[i]字符出发时，匹配到j位置的字符发现与match中的字符不一致，

现在有match字符串的next数组，next[j-i]表示 match[0..j-i-1] 这段字符前缀与后缀的最长匹配

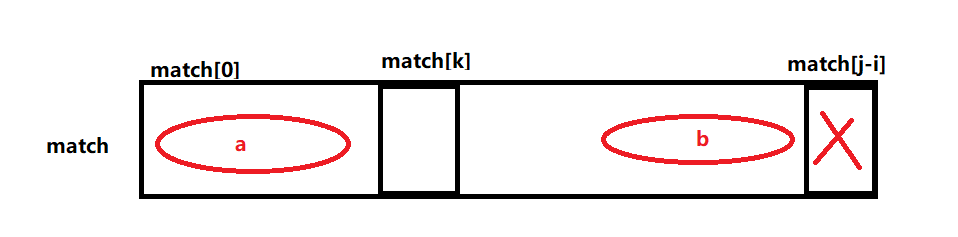
下一次匹配检查让str[i]与match[k]进行匹配检查，对于match[] 来说，相当于向右滑动，让match[k]滑动到与str[j]在同一个位置上，然后进行后续的匹配检查，一直进行这样的滑动匹配，直到在str某一位置把match完全匹配，说明str中有match，如果滑动到最后也没匹配出来，说明str中没有match

为什么中间不要检查，必然匹配不了呢

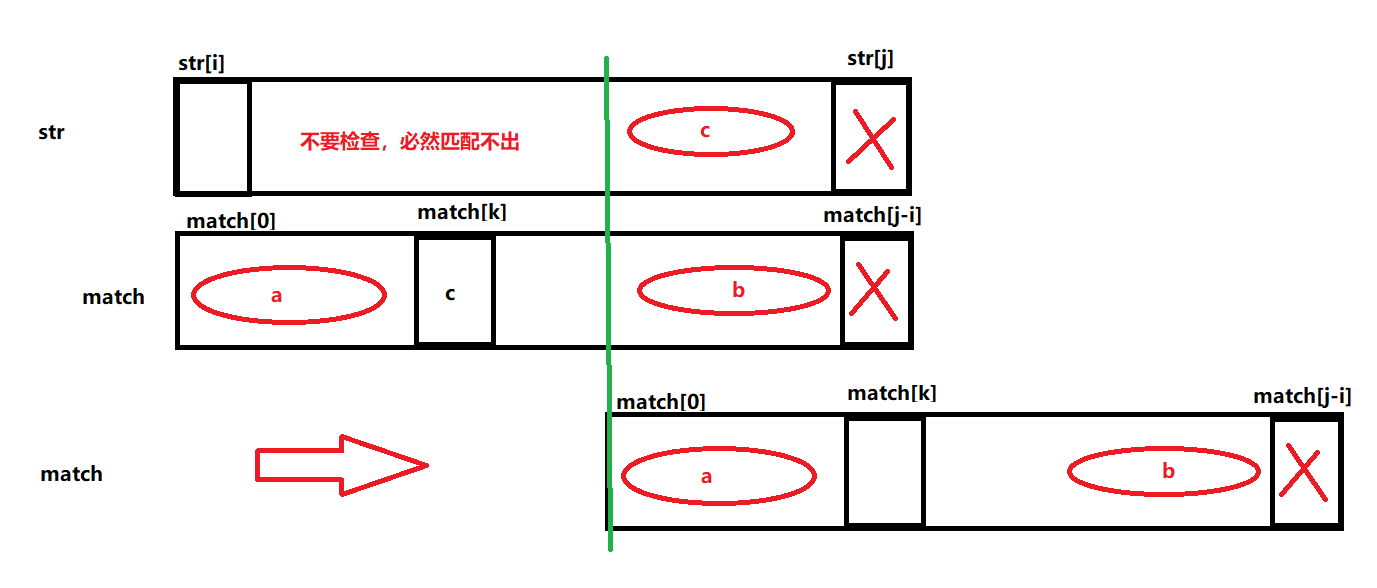
在str[j]位置匹配失败，b区域与c区域相等，a区域与b区域相等，必然a区域与c区域相等

中间的区域不需要检查，直接将a区域滑动到与c区域对齐即可

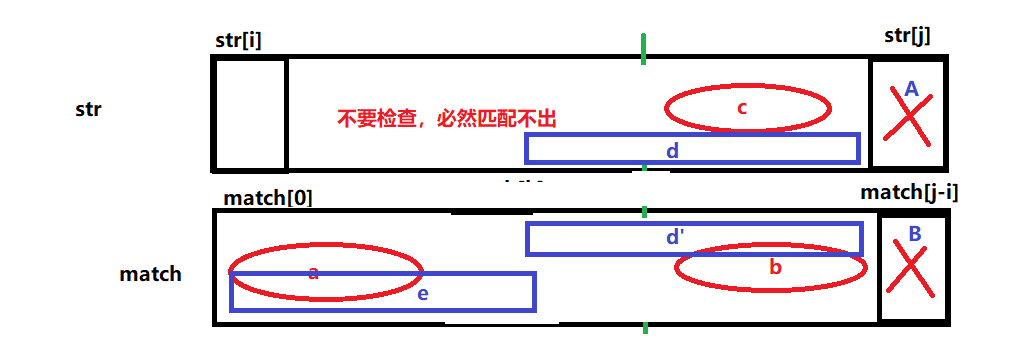
假设d区域开始字符是不要检查区域的一个位置，如果这位置开始匹配出match，整个d区域要和从match[0]开始的e区域匹配，d和e的长度一样，d区域比c区域大，e区域比a区域大

时间复杂度

str 匹配位置是不退回的，match 一直向右移动，如果在str某个位置完全匹配出match，整个过程停止，否则match滑动到str最右侧停止，滑动最大长度为 $N$，所以时间复杂度为 $O(N)$

算法实现

getNext

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public int[] getNext(char[] match) {
    if (match.length == 1) {
        return new int[]{-1};
    }
    int[] next = new int[match.length];
    next[0] = -1;
    next[1] = 0;
    int i = 2;
    int j = 0;

    while (i < next.length) {
        if (match[i - 1] == match[j]) { // 相等，匹配下一个
            next[i++] = ++j;
        } else if (j > 0) { // 不相等往前跳，继续匹配
            j = next[j];
        } else { // 来到最左边情况，说明i之前字符不存在前后缀匹配情况，匹配下一个
            next[i++] = 0;
        }
    }
    return next;
}

KMP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public int KMP(String str, String match) {
    if (str == null || match == null ||
            match.length() < 1 || str.length() < match.length()) {
        return -1;
    }
    char[] mainStr = str.toCharArray();
    char[] subStr = match.toCharArray();
    int i = 0;
    int j = 0;
    int[] next = getNext(subStr);
    while (i < mainStr.length && j < subStr.length) {
        if (mainStr[i] == subStr[j]) {
            i++;
            j++;
        } else if (next[j] == -1) { // 往前跳到开头都匹配不出来，找主串下一个位置开始匹配
            i++;
        } else { // 当前匹配不出来且没有跳到子串开头，往前跳
            j = next[j];
        }
    }
    return j == subStr.length ? i - j : -1;
}