准备和应对算法

平时如何刷算法

根据专题进行分类刷题

面试如何应对算法

  1. 理解问题，复述问题进而明确问题
  2. 进一步确认问题，大胆说出想法，逐步找到最优想法
  3. 初步设计，先写整体，再考虑边界
  4. 测试检验，评判性能，优化解法

数据结构与算法基础

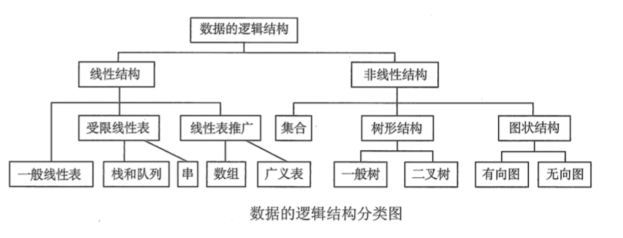
数据结构类型

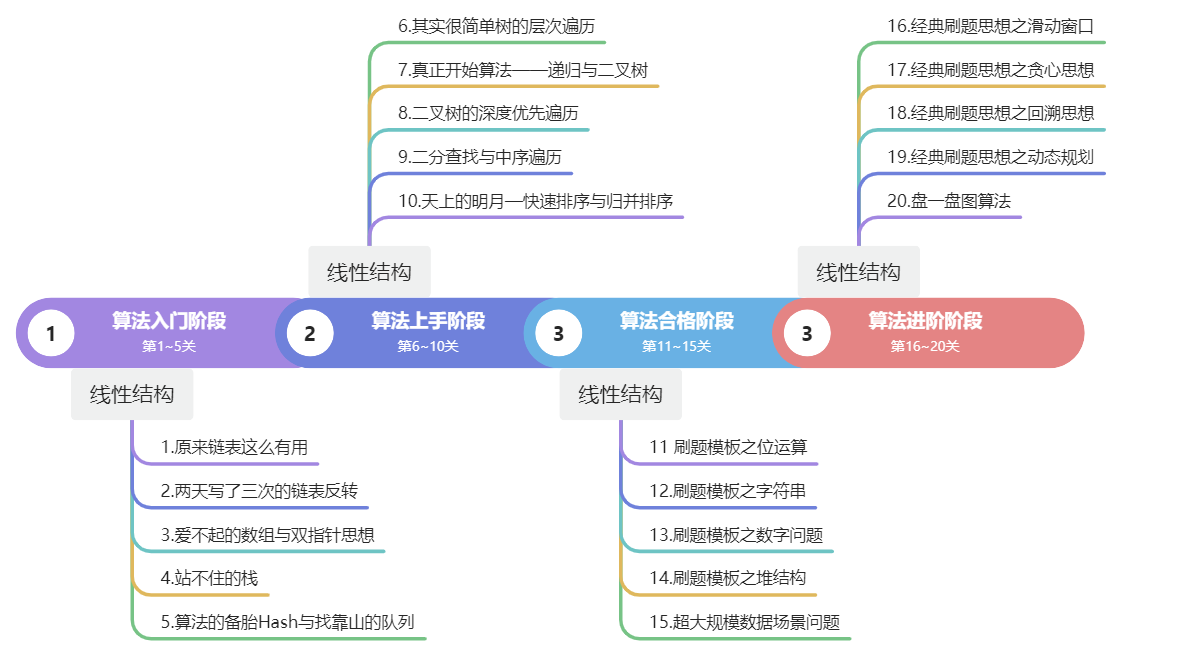
进度安排

体系脉络

时间和空间复杂度

时间复杂度

常数阶：一般顺序执行并且只执行一次的代码。

1
2
3
4
sum = sum + 1;
sum = sum + 2;
sum = sum + 3;
sum = sum + 4;

线性阶：执行的次数随着问题规模是线性变化的。

1
2
3
for (int i = 0; i < n; i++) {
    // todo
}

平方阶：主要是双层嵌套循环。

1
2
3
4
5
for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
        // todo 时间复杂度为 1 的程序
    }
}

对数阶 

1
2
3
4
5
6
7
int count = 1;
int n = 64;
int items = 0;
while (count < n) {
    count = count * 2; // todo 注意的是此行的执行次数与 n 的关系
    items++;
}

但凡处理时间复杂度，注意代码体与循环结束条件之间的关系：

todo 执行次数 1 2 3 4 5
count 1 2 4 8 16

当 todo 要执行第 7 次时，不满足 count < n，因此执行次数与 n 的关系是：

时间复杂度练习

  1. $n-1$

    1
    2
    3
    4
    5
    6
    int i = 1, k = 0;

    while (i <= n-1) {
        @ k += 10 * i;
        i++;
    }

  2. $n-1$

    1
    2
    3
    4
    5
    int i = 1, k = 0;
    do {
        @ k += 10 * i;
        i++;
    } while (i <= n-1)

  3. $n-1$

    1
    2
    3
    4
    5
    6
    int i = 1, k = 0;

    while (i <= n-1) {
        i++;
        @ k += 10 * i;
    }

  4. $\frac{n(n+1)}{2}$

    1
    2
    3
    4
    5
    6
    int k = 0;
    for (int i = 1; i <= n; i++) {
        for (int j = i; j <= n; j++) {
            @ k++;
        }
    }

  5. $\frac{1}{12}{n(n+1)(2n+4)}$

    1
    2
    3
    4
    5
    6
    7
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= i; j++) {
            for (int k = 1; k <= j; k++) {
                @ x += delta;
            }
        }
    }

  6. $n$

    1
    2
    3
    4
    5
    6
    int i = 1, j = 0;
    while (i + j <= n) {
        @ if (i > j) 
             j++;
        else i++;
    }

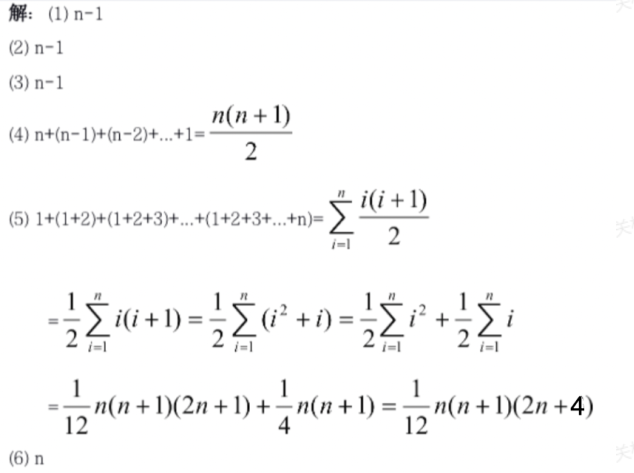
空间复杂度

空间复杂度是指申请额外空间数来处理事情

  • 申请若干变量，则 $O(1)$
  • 申请数组、链表、队列、栈、Hash，则 $O(n)$
  • 申请二维数组，则 $O(n^2)$