算法通关 1 - 链表专题Ⅰ

总结

• 常见的数据结构： 数组、链表、栈、队列、哈希、树、堆
• 常用的算法思想： 查找、排序、双指针、递归、迭代、分治、贪心、回溯、动态规划

链表专题Ⅰ—链表基础

内容概览

题目	难度
链表遍历	简单
链表插入	简单
删除链表	简单
链表头插法	简单
链表尾插法	简单

参考资料

1.Java 是如何构造链表的

2.一道题透彻理解链表是什么

3.闭着眼都要会—链表增删改查

4.大厂都是如何如何考链表的

5.手写小红书考过的的链表求并集算法

单链表

单链表包含若干节点，每个节点具有指向后继结点的 next 指针，最后一个节点的 next 指向 NULL。

正确示范

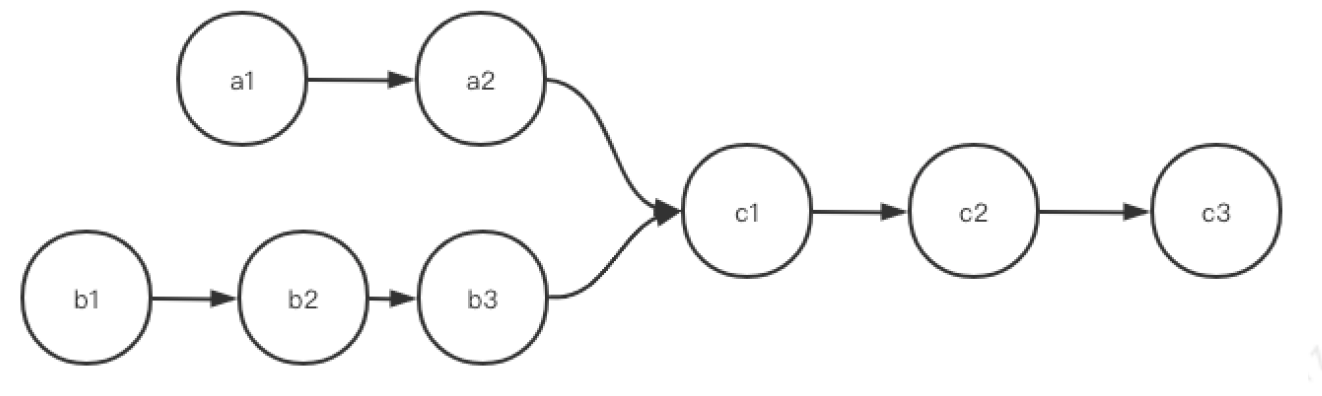
错误示范

虚拟节点和头节点

节点和头节点

链表中每个节点都由值和指向下一个节点的地址组成，对于单链表，第一个元素节点称为头节点

虚拟节点

• 即 dummyNode，其 next 指针指向 head
• 如果获取 head 节点，或者从方法里返回时，使用 dummyNode.next
• dummyNode 的 val 不会被使用，通常初始化成 0 或 -1

创建链表

JVM 如何构建链表的？

JVM 下栈区存放实际对象的引用地址，堆区存放创建的对象：

public class Course {
    Teacher teacher;
    Student student;
}

此时的 teacher 和 student 就是指向堆的引用，若我们这样定义：

public class Course {
    int val;
    Course next;
}

此时 next 指向下一个同为 Course 类的对象

这里通过栈中引用找到 val(1)，然后 val(1) 节点存放指向 val(2) 的地址，val(3) 存放指向 val(4) 的地址。

DEBUG 图示：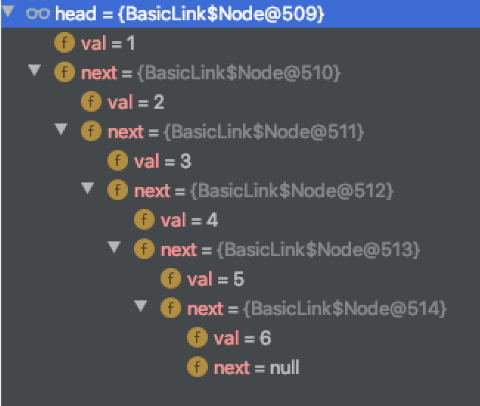

链表从 head 开始，逐个访问，每次访问的对象类型完全一样的。

根据面向对象理论，Java 规范的链表定义：

public class ListNode {

    private int data;
    private ListNode next;

    public ListNode(int data) {
        this.data = data;
    }
    
    public int getData() {
        return data;
    }
    
    public void setData(int data) {
        this.data = data;
    }
    
    public ListNode getNext() {
        return next;
    }

    public void setNext(ListNode next) {
        this.next = next;
    }
}

LeetCode 链表结构参考：

public class ListNode {

    private int val;
    private ListNode next;

    ListNode(int x) {
        this.data = x;
        next = null;
    }

}
ListNode listnode = new ListNode(1);

LeetCode 结构违背面向对象设计要求，代码更为精简，算法题目中应用广泛。

链表增删改查

遍历链表

对于单链表，无论进行何操作，操作后是否还能找到表头非常重要。

// 遍历链表长度
public int getListLength(ListNode head) {
    int length = 0;
    ListNode node = head;
    
    while (node != null) {
        length++;
        node = node.next;
    }
    return length;
} 

插入链表

单链表的插入需要考虑头部、中部、尾部情况。

在单链表的表头插入：

从表头插入，不要忘记 head 重新指向表头。

// 新建点指向 head
newNode.next = head;
// 再将 head 指向链表首元素
head = newNode;

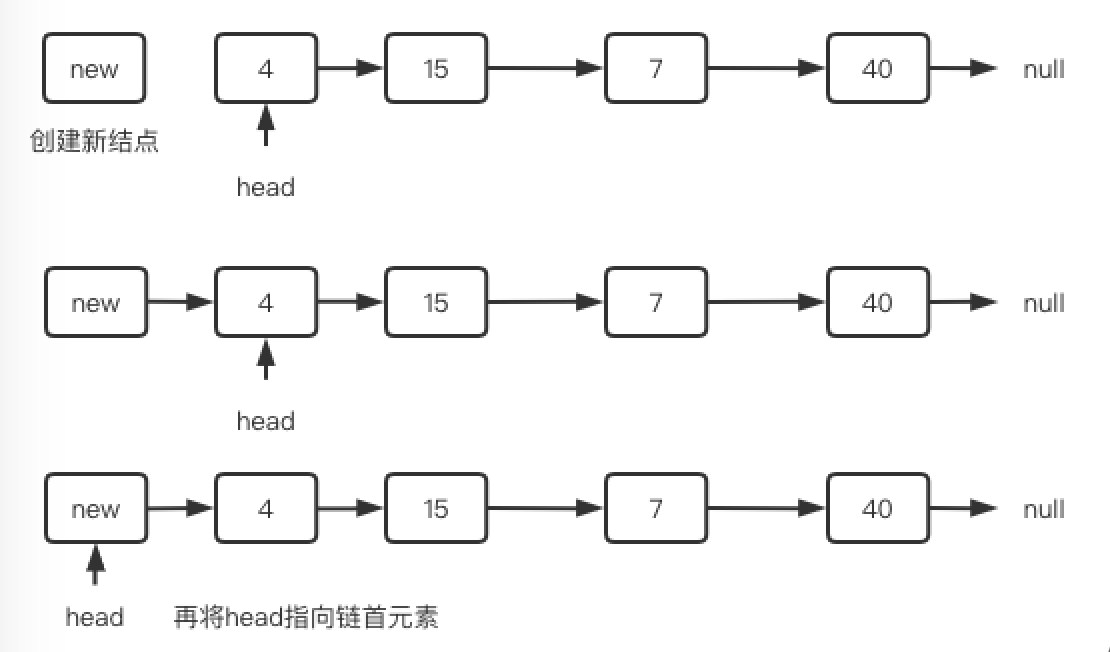
在单链表的中间插入：

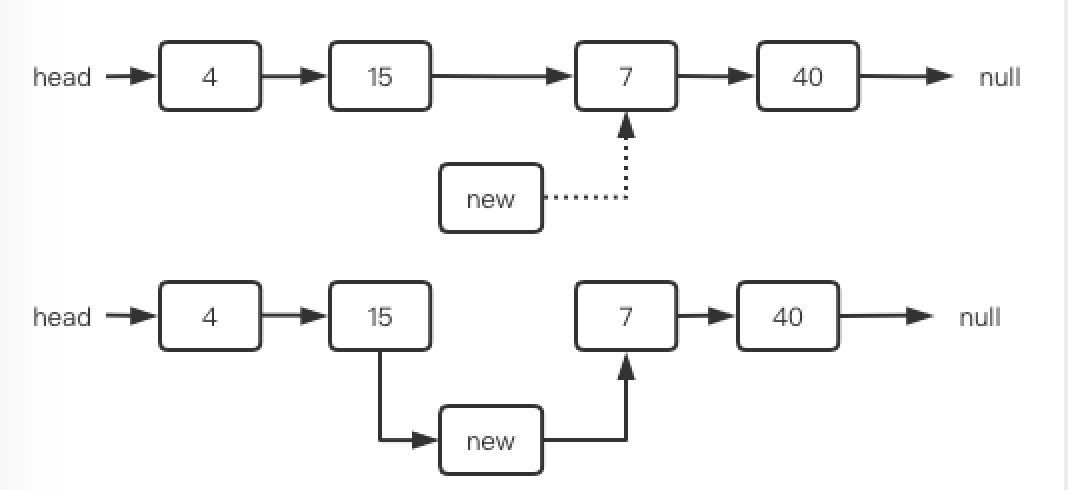
在中间位置插入，必须遍历找到插入位置，然后将当前位置接入到前驱节点和后继节点之间，但是到了该位置后无法获取前驱节点，为此我们在目标节点的前一个位置停下，使用 cur.next 值进行判断：
例如我们在下图中 7 的前面插入，当 cur.next = node(7) 就应该停下来，具体操作如下。

// 在 7 前面插入节点，则 cur.next = node(7) 就应该停下，此时 cur.val = 15
// 此时先让 newNode.next = node(15).next
newNode.next = node(15).next;
// 然后 node(15).next = newNode，顺序一定不能出错
node(15).next = newNode;

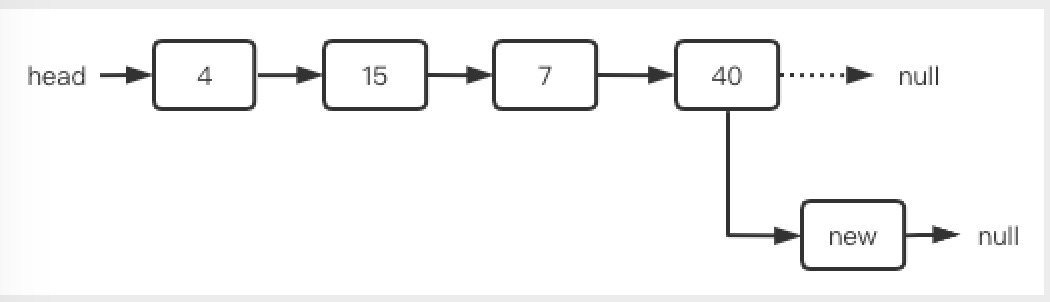
在单链表的尾部插入：

// 尾节点指向新节点
node(tail).next = newNode;

单链表插入方法实现：

/**
 * 链表插入
 *
 * @param head 链表头节点
 * @param nodeInserted 待插入节点
 * @param position 待插入位置，从 1 开始
 * @return 插入后得到的链表头节点
 */
public ListNode insertListNode(ListNode head, ListNode nodeInserted, int position) {
    
    // 边界判断
    if (head == null) {
        return nodeInserted;
    }
    // 已经存放的元素个数
    int size = getListLength(head);

    // 边界判断
    if (position > size + 1 || position < 1) {
        System.out.println("位置参数越界");
        return head;
    }

    // 头部插入
    if (position == 1) {
        nodeInserted.next = head;
        head = nodeInserted;
        return head;
    }
    
    ListNode pNode = head;
    int count = 1;

    // 由于 position 被 size 限制住，无需考虑 pNode = null
    while (count < position - 1) { // 寻找插入位置（目标位置的前一个位置）
        pNode = pNode.next;
        count++;
    }

    // 插入节点
    nodeInserted.next = pNode.next;
    pNode.next = nodeInserted;
    
    return head;
}

扩展：若链表要求单调递增，请将元素插入合适位置，并使链表仍程单调递增，请写出算法实现？

删除链表

单链表的删除需要考虑头部、中部、尾部情况。

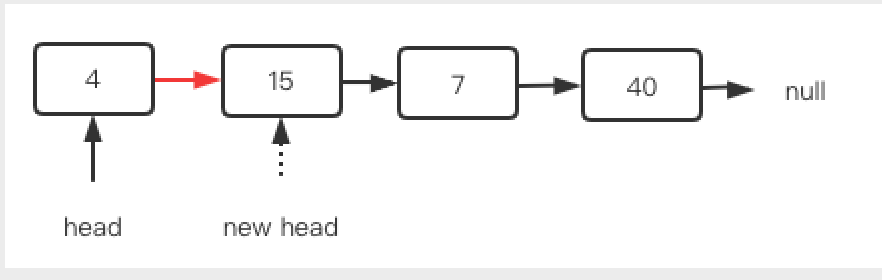
删除单链表的表头节点：

// 一般执行 `head = head.next` 即可。
head = head.next

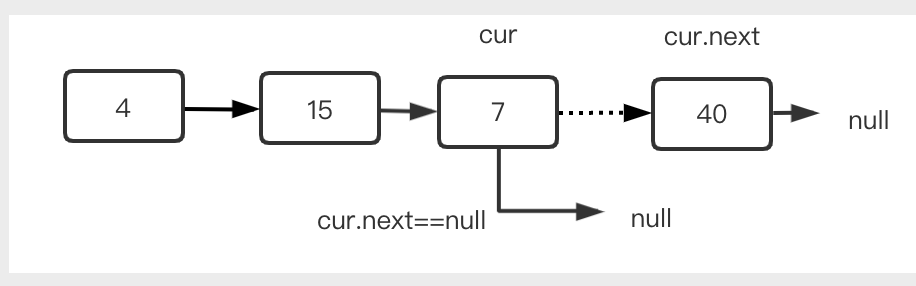
删除单链表的表尾节点：

找到待删除节点的前驱节点，然后执行 cur.next = null 即可。
例如删除 40，器前驱为 7，遍历时需要判断 cur.next 是否为 40，然后执行 cur.next = null

删除单链表的中间节点：

删除中间节点时，使用 cur.next 比较，找到位置后将 cur.next 的值 更新为 cur.next.next

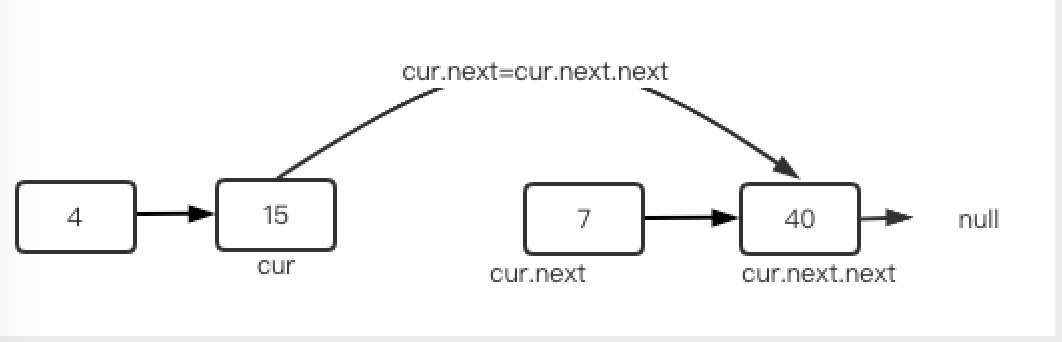
单链表删除方法实现：

/**
 * 删除节点
 *
 * @param head 链表头节点
 * @param position 待删除节点位置，从 1 开始
 * @return 删除后的链表头节点
 */
public ListNode deleteListNode(ListNode head, int position) {
    
    // 边界判断
    if (head == null) {
        return null;
    }

    int size = getListLength(head);

    // 边界判断（注意这里是 size，不是 size + 1）
    if (position > size || position < 1) {
        System.out.println("位置越界");
        return head;
    }

    // 头部删除
    if (position == 1) {
        return head.next;
    } else { // 其他情况
        ListNode cur = head;
        int count = 1;
        while (count < position - 1) { // 寻找删除位置（目标位置的前一个位置）
            cur = cur.next;
            count++;
        }
        // 删除节点
        ListNode curNode = cur.next;
        cur.next = curNode.next;
    }
    
    return head;
}

扩展：若链表是有序的，请删除某元素，并使链表仍程单调递增，请写出算法实现？

头插法和尾插法

问题

假设有 n 个元素存储在数组 a 中，使用尾插法和头插法建立单链表 C

尾插法

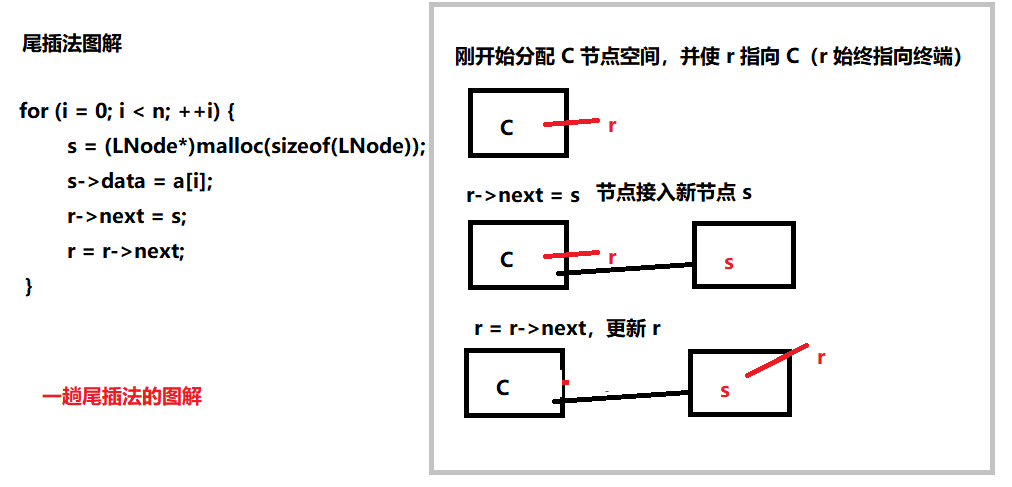
void createListR(LNode *&C, int a[], int n) {
    LNode *s, *r; // s 指向新申请的节点，r 始终指向 C 的终端节点
    int i;
    C = (LNode*)malloc(sizeof(LNode)); // 申请 C 的头节点空间
    C->next  = NULL;
    r = C; // r 指向头节点，因为此时头节点就是终端节点
    for (i = 0; i < n; ++i) { // 循环申请 n 个节点来接受数组 a 的元素
        s = (LNode*)malloc(sizeof(LNode)); // s 指向新申请的节点
        s->data = a[i]; // 用新申请的节点来接受 a 的一个元素
        r->next = s; // 用 r 来接纳新节点
        r = r->next; // r 指向尾节点，以便于接纳下一个到来的节点
    }
    r->next = NULL; //数组 a 中所有的元素存人 C 中，C 的终端节点的指针域置位 NULL，C 建立完成
}

头插法

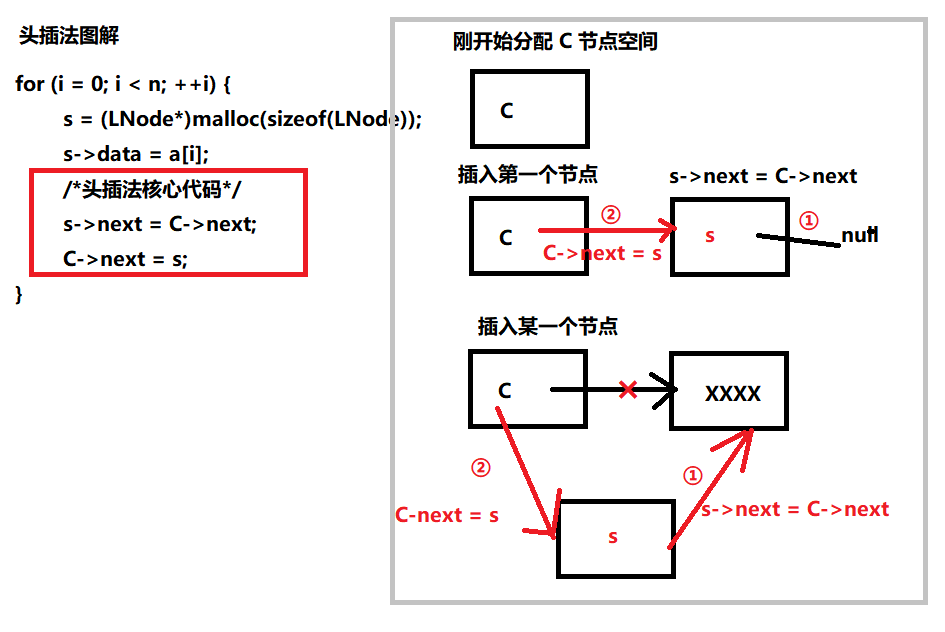
void createListF(LNode *&C, int a[], int n) {
    LNode *s; // s 指向新申请的节点 
    int i;
    C = (LNode*)malloc(sizeof(LNode)); // 申请 C 的头节点空间
    C->next  = NULL;
    for (i = 0; i < n; ++i) { // 循环申请 n 个节点来接受数组 a 的元素
        s = (LNode*)malloc(sizeof(LNode)); // s 指向新申请的节点
        s->data = a[i]; // 用新申请的节点来接受 a 的一个元素
        /*头插法核心代码*/
        s->next = C->next; // s 所指新节点的指针域 next 指向 C 中的开始节点
        C->next = s; // 头节点的指针域 next 指向 节点，使得 s 成为新的开始节点
    }
}

链表专题Ⅰ—链表强化

内容概览

题目	难度
两个链表第一个公共子节点	简单
判断链表是否是回文序列	中等
合并两个有序链表	简单
合并两个链表	简单
合并 K 个有序链表	中等
寻找链表的中间节点	简单
寻找倒数第 K 个元素	简单
旋转链表	中等
删除链表特定节点	简单
删除链表倒数第 n 个节点	简单
删除链表重复元素（重复的保留一个）	简单
删除链表重复元素（重复的都删除）	中等

节点结构

public class ListNode {

    public int val;
    public ListNode next;

    ListNode(int x) {
        val = x;
        next = null;
    }
}

两个链表第一个公共子节点

LCR 023. 相交链表

160. 相交链表

题目

输入两个链表，请找出它们的第一个公共节点。两个链表的头节点都是已知的，相交之后成为一个单链表，但是相交的位置未知，并且相交之前的节点数是未知的，请设计算法包找出两个链表的合并点

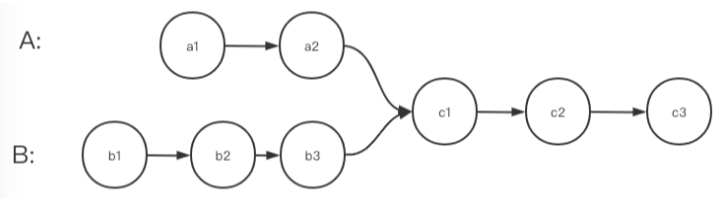
【推荐】使用哈希集合

算法思想

判断两个链表是否相交，可以使用哈希集合存储链表节点。

首先遍历链表 headA，并将链表 headA 中的每个节点加入哈希集合中。然后遍历链表 headB，对于遍历到的每个节点，判断该节点是否在哈希集合中：

• 如果当前节点不在哈希集合中，则继续遍历下一个节点；
• 如果当前节点在哈希集合中，则后面的节点都在哈希集合中，即从当前节点开始的所有节点都在两个链表的相交部分，因此在链表 headB 中遍历到的第一个在哈希集合中的节点就是两个链表相交的节点，返回该节点。

如果链表 headB 中的所有节点都不在哈希集合中，则两个链表不相交，返回 null。

参考答案

public ListNode getIntersectionNode(ListNode headA, ListNode headB) {

    // 将链表 A 装入集合
    Set<ListNode> set = new HashSet<>();
    ListNode temp = headA;
    while (temp != null) {
        set.add(temp);
        temp = temp.next;
    }
    
    // 校验操作
    temp = headB;
    while (temp != null) {
        if (set.contains(temp)) {
            return temp;
        }
        temp = temp.next;
    }
    return null;
}

【推荐】使用双指针

使用双指针的方法，可以将空间复杂度降至 $O(1)$

算法思想

只有当链表 headA 和 headB 都不为空时，两个链表才可能相交。因此首先判断链表 headA 和 headB 是否为空，如果其中至少有一个链表为空，则两个链表一定不相交，返回 null。

当链表 headA 和 headB 都不为空时，创建两个指针 pA 和 pB，初始时分别指向两个链表的头节点 headA 和 headB，然后将两个指针依次遍历两个链表的每个节点

• 每步操作需要同时更新指针 pA 和 pB。
• 如果指针 pA 不为空，则将指针 pA 移到下一个节点；如果指针 pB 不为空，则将指针 pB 移到下一个节点
• 如果指针 pA 为空，则将指针 pA 移到链表 headB 的头节点；如果指针 pB 为空，则将指针 pB 移到链表 headA 的头节点。
• 当指针 pA 和 pB 指向同一个节点或者都为空时，返回它们指向的节点或者 null。

证明过程

LCR 023. 相交链表

下面提供双指针方法的正确性证明。考虑两种情况，第一种情况是两个链表相交，第二种情况是两个链表不相交。

情况一：两个链表相交

链表 headA 和 headB 的长度分别是 m 和 n。假设链表 headA 的不相交部分有 a 个节点，链表 headB 的不相交部分有 b 个节点，两个链表相交的部分有 c 个节点，则有 $a+c=m$，$b+c=n$。

• 如果 $a=b$，则两个指针会同时到达两个链表相交的节点，此时返回相交的节点；
• 如果 $a≠b$，则指针 pA 会遍历完链表 headA，指针 pB 会遍历完链表 headB，两个指针不会同时到达链表的尾节点，然后指针 pA 移到链表 headB 的头节点，指针 pB 移到链表 headA 的头节点，然后两个指针继续移动，在指针 pA 移动了 $a+c+b$ 次、指针 pB 移动了 $b+c+a$ 次之后，两个指针会同时到达两个链表相交的节点，该节点也是两个指针第一次同时指向的节点，此时返回相交的节点。

情况二：两个链表不相交

链表 headA 和 headB 的长度分别是 m 和 n。考虑当 $m=n$ 和 $m≠n$ 时，两个指针分别会如何移动：

• 如果 $m=n$，则两个指针会同时到达两个链表的尾节点，然后同时变成空值 null，此时返回 null；
• 如果 $m≠n$，则由于两个链表没有公共节点，两个指针也不会同时到达两个链表的尾节点，因此两个指针都会遍历完两个链表，在指针 pA 移动了 $m+n$ 次、指针 pB 移动了 $n+m$ 次之后，两个指针会同时变成空值 null，此时返回 null。

参考答案

public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    // base case
    if (headA == null || headB == null) {
        return null;
    }
    // 哨兵节点
    ListNode pA = headA, pB = headB;
    // 判断逻辑
    while (pA != pB) {

        // 如果指针 pA 不为空，则指向下一个位置；如果为空，则指向链表 B 的头节点
        pA = pA == null ? headB : pA.next;
        // 如果指针 pB 不为空，则指向下一个位置；如果为空，则指向链表 A 的头节点
        pB = pB == null ? headA : pB.next;
    }
    return pA;
}

判断链表是否是回文序列

234. 回文链表

题目

【LeetCode 234】：给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

思路 1：（暴力方案 | 利用栈）

1. 将链表元素全部压栈
2. 然后进行出栈操作，出栈同时遍历链表
3. 比较出栈元素和遍历元素值
4. 直到出栈完成，如果中途出现不相等情况，说明不是回文链表

思路 2：（优化方案 | 利用栈）

1. 第一次遍历整个链表，获取链表总长度
2. 第二次遍历链表，遍历链表同时进行压栈操作
3. 到达链表长度一半后不进行压栈操作，而是一边出栈一边遍历
4. 期间比较两个操作下的元素是否相等，直到出栈完成
5. 如果出现不相等情况，说明不是回文链表

思路 3：（优化方案 | 利用栈）

1. 第一次遍历整个链表，获取链表总长度，遍历链表同时压栈处理元素
2. 第二次遍历链表，只需要遍历一半链表（同时仅需出栈一半元素）
3. 期间比较两个操作下的元素是否相等，直到出栈完成
4. 如果出现不相等情况，说明不是回文链表

思路 4：（暴力方案 | 反转链表）

1. 开辟新存储空间，存储反转后的链表
2. 遍历两个链表进行比较元素

思路 5：（优化方案 | 反转链表）

1. 第一次遍历整个链表，获取链表长度
2. 开辟存储空间准备存储半段链表，反转前半段链表
3. 比较新的链表和剩下的链表的元素

思路 6：（优化方案 | 快慢指针、反转链表）

1. 使用快慢指针找到中点
2. 反转中点后的链表
3. 比较原始链表的前半段和反转后的后半段的元素

思路 7：（优化方案 | 递归）

如果使用递归反向迭代节点，同时使用递归函数外的变量向前迭代，就可以判断链表是否为回文。

【推荐】使用快慢指针

算法思路 （若链表有奇数个节点，则中间的节点应该看作是前半部分。）

将链表的后半部分反转，然后将前半部分和后半部分进行比较。比较完成后应该将链表恢复原样。虽然不需要恢复也能通过测试用例，但是使用该函数的人通常不希望链表结构被更改。

1. 找到前半部分链表的尾节点
2. 反转后半部分链表
3. 判断是否回文
4. 恢复链表
5. 返回结果

找到前半部分链表的尾节点

• 使用快慢指针在一次遍历中找到
• 慢指针一次走一步，快指针一次走两步，快慢指针同时出发
• 当快指针移动到链表的末尾时，慢指针恰好到链表的中间。通过慢指针将链表分为两部分。
  若链表有奇数个节点，则中间的节点应该看作是前半部分。

反转后半部分链表

可以使用「206. 反转链表」问题中的解决方法来反转链表的后半部分。

参考答案

// 快慢指针 + 反转链表
public boolean isPalindrome(ListNode head) {

    // base case
    if (head == null) {
        return true;
    }

    // 找到链表中点（前半部分链表的尾节点）
    ListNode firstHalfEnd = endOfFirstHalf(head);
    // 反转链表（将后半部分链表进行反转）
    ListNode secondHalfStart = reverseList(firstHalfEnd.next);

    // 回文判断
    ListNode p1 = head; // p1 指向原始链表表头
    ListNode p2 = secondHalfStart; // p2 指向反转后的链表表头
    boolean result = true;

    while (result && p2 != null) {
        if (p1.val != p2.val) {
            result = false;
        }
        p1 = p1.next;
        p2 = p2.next;
    }

    // 还原链表
    firstHalfEnd.next = reverseList(secondHalfStart);

    return result;
}

// 反转链表（默认不带虚拟节点）
private ListNode reverseList(ListNode head) { // 头插法
    ListNode L = null;
    ListNode p = head;

    while (p != null) {

        // 保存下一个节点位置
        ListNode q = p.next;
        p.next = L;
        L = p;
        p = q;

    }
    return L;
}

// 快慢指针遍历中点
private ListNode endOfFirstHalf(ListNode head) {

    // 快指针
    ListNode fast = head;
    // 慢指针
    ListNode slow = head;

    // 如果有两个中间结点，则返回的是第 1 个中间结点。
    while (fast.next != null && fast.next.next != null) {
        fast = fast.next.next;
        slow = slow.next;
    }

    return slow;
}

// 反转链表（扩展：如果带虚拟节点可以这样写：）
private ListNode reverseList(ListNode head) { // 头插法

    ListNode L = new ListNode(0);
    // 将虚拟节点挂到表头
    L.next = head;
    // 定义哨兵指针
    ListNode p = head; // p 指向虚拟节点后的第一个元素
    // q 永远指向 p 的后继，方便下次反转
    ListNode q = null;

    // 断链操作
    L.next = null;
    while (p != null) {
        q = p.next;
        p.next = L.next;
        L.next = p;
        p = q;
    }

    return L.next;
}

使用递归

算法思想

为想出使用空间复杂度为 $O(1)$ 的算法，你可能想过使用递归来解决，但是这仍然需要 $O(n)$ 的空间复杂度。

递归为我们提供了一种优雅的方式来方向遍历节点。

function print_values_in_reverse(ListNode head)
    if head is NOT null
        print_values_in_reverse(head.next)
        print head.val

如果使用递归反向迭代节点，同时使用递归函数外的变量向前迭代，就可以判断链表是否为回文。

算法原理

currentNode 指针是先到尾节点，由于递归的特性再从后往前进行比较。frontPointer 是递归函数外的指针。
若 currentNode.val != frontPointer.val 则返回 false。反之，frontPointer 向前移动并返回 true。

算法的正确性在于递归处理节点的顺序是相反的（回顾上面打印的算法），而我们在函数外又记录了一个变量，因此从本质上，我们同时在正向和逆向迭代匹配。

具体请看：官方动画解释

class Solution {
    private ListNode frontPointer;

    private boolean recursivelyCheck(ListNode currentNode) {
        if (currentNode != null) {
            if (!recursivelyCheck(currentNode.next)) {
                return false;
            }
            if (currentNode.val != frontPointer.val) {
                return false;
            }
            frontPointer = frontPointer.next;
        }
        return true;
    }

    public boolean isPalindrome(ListNode head) {
        frontPointer = head;
        return recursivelyCheck(head);
    }
}

合并链表专题

合并两个有序链表

21. 合并两个有序链表

题目

【LeetCode 21】：将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

【推荐】迭代归并

算法思想

构建新链表，分别遍历两个链表，每次选择最小的节点接到新链表上，不断迭代直到结束

public ListNode mergeTwoLists(ListNode list1, ListNode list2) {

    // 新链表头节点（虚拟节点）
    ListNode L = new ListNode(0);
    // 保存尾指针
    ListNode tail = L;

    // 尾插法
    while (list1 != null && list2 != null) { // 两个链表都不为空时

        if (list1.val < list2.val) {
            tail.next = list1;
            list1 = list1.next;
        } else if (list1.val > list2.val) {
            tail.next = list2;
            list2 = list2.next;
        } else { // 相等时，两个节点都接上去
            tail.next = list1;
            list1 = list1.next;
            tail = tail.next;
            tail.next = list2;
            list2 = list2.next;
        }
        tail = tail.next;
    }

    while (list1 != null) { // L1 链表未遍历完时
        tail.next = list1;
        list1 = list1.next;
        tail = tail.next;
    }

    while (list2 != null) { // L2 链表未遍历完时
        tail.next = list2;
        list2 = list2.next;
        tail = tail.next;
    }

    return L.next;
}

迭代优化

• 优化 1：第一处 while 三种情况中的如果出现两个相同元素，将此处情况归并到第一种情况 if (list1.val <= list2.val)，那么另一个相同的元素会被第二种情况处理掉。
  比如 list1[1, 5, 8, 2] 和 list2[2, 5, 9, 13]，当两个链表都到元素 5 时，此时先合并 list1 中的 node(5)，然后 list 走下一个元素 8，此时 list2 停留在 node(5)，它将会走第二个情况
• 优化 2：循环终止时， list1 和 list2 至多有一个是非空的。由于输入的两个链表都是有序的，所以不管哪个链表非空，它包含的所有元素都比前面已经合并链表中的所有元素都要大，因此只需要简单地将非空链表接在合并链表的后面，并返回合并链表即可。

public ListNode mergeTwoLists(ListNode list1, ListNode list2) {

    // 新链表头节点（虚拟节点）
    ListNode L = new ListNode(0);
    // 保存尾指针
    ListNode tail = L;

    while (list1 != null && list2 != null) {
        if (list1.val <= list2.val) {
            tail.next = list1;
            list1 = list1.next;
        } else {
            tail.next = list2;
            list2 = list2.next;
        }
        tail = tail.next;
    }

    // 合并后 list1 和 list2 最多只有一个还未被合并完
    // 我们直接将链表末尾指向未合并完的链表即可
    tail.next = list1 == null ? list2 : list1;
    
    return L.next;
}

递归归并

递归

如果 list1 或者 list2 一开始就是空链表 ，那么没有任何操作需要合并，所以我们只需要返回非空链表。否则，我们要判断 list1 和 list2 哪一个链表的头节点的值更小，然后递归地决定下一个添加到结果里的节点。如果两个链表有一个为空，递归结束。

public ListNode mergeTwoLists(ListNode list1, ListNode list2) {

    if (list1 == null) {
        return list2;
    } else if (list2 == null) {
        return list1;
    } else if (list1.val < list2.val) {
        list1.next = mergeTwoLists(list1.next, list2);
        return list1;
    } else {
        list2.next = mergeTwoLists(list1, list2.next);
        return list2;
    }
}

合并 K 个链表

23. 合并 K 个升序链表

题目

【LeetCode 23】：给你一个链表数组，每个链表都已经按升序排列。请你将所有链表合并到一个升序链表中，返回合并后的链表。

【推荐】顺序归并

算法思想

使用 ans 维护以及合并的链表，第 i 循环把第 i 个链表和 ans 合并，答案保存到 ans 中

public ListNode mergeKLists(ListNode[] lists) {

    ListNode ans = null;

    for (int i = 0; i < lists.length; i++) {
        ans = mergeTwoLists(ans, lists[i]);
    }
    return ans;
}

public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
    // base case
    if (list1 == null || list2 == null) {
        return list1 != null ? list1 : list2;
    }
    ListNode L = new ListNode(0);
    ListNode tail = L;

    while (list1 != null && list2 != null) {
        if (list1.val <= list2.val) {
            tail.next = list1;
            list1 = list1.next;
        } else {
            tail.next = list2;
            list2 = list2.next;
        }
        tail = tail.next;
    }
    tail.next = list1 != null ? list1 : list2;

    return L.next;
}

【推荐】分治归并

【归并排序】算法思想

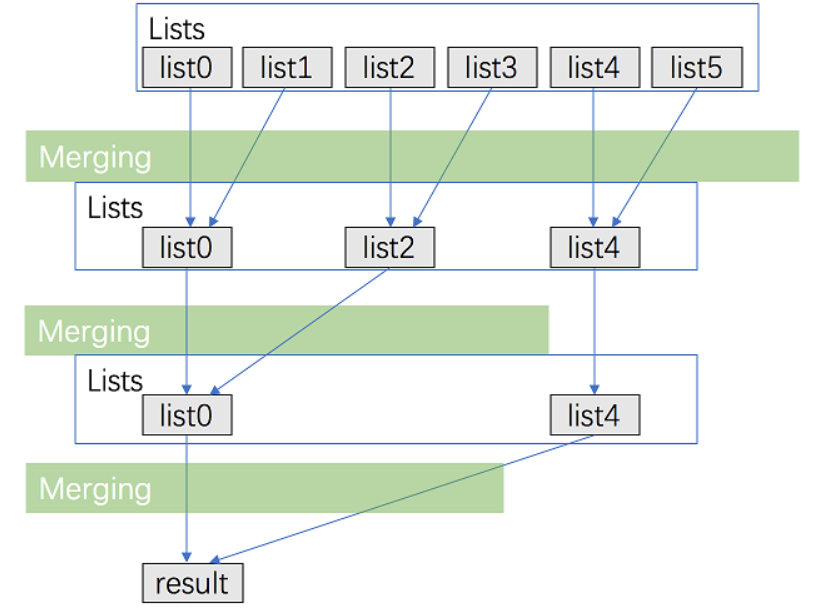
采用分治发优化顺序合并：

• 将 k 个链表配对并将同一对中的链表合并
• 第一轮合并后，k 个链表合并成 k/2 个链表，然后是 k/4 个链表，8/k 个链表等；
• 重复这一过程，直到得到最终的有序链表

public ListNode mergeKLists(ListNode[] lists) {
    return merge(lists, 0, lists.length - 1);
}

public ListNode merge(ListNode[] lists, int begin, int end) {
    // 递归终止条件 1  
    if (begin == end) {
        return lists[begin];
    }
    // 递归终止条件 2
    if (begin > end) {
        return null;
    }

    // 划分左右子链表
    int mid =  begin + ((end - begin) >> 1);
    // 递归归并左半部分链表
    ListNode leftMerge = merge(lists, begin, mid);
    // 递归归并右半部分链表
    ListNode rightMerge = merge(lists, mid + 1, end);
    
    return mergeTwoLists(leftMerge, rightMerge);

}

小顶堆归并

算法思想

• 维护当前每个链表未合并的元素的最前面一个，k 个链表就最多有 k 个满足这样条件的元素
• 每次在这些元素里面选取 val 属性最小的元素合并到答案中
• 使用小顶堆数据结构选取最小元素

// 优先队列合并
class Status implements Comparable<Status> { // 实现了 Comparable 接口的 Node

    // Node.val
    int val;
    // Node
    ListNode ptr;

    Status(int val, ListNode ptr) {
        this.val = val;
        this.ptr = ptr;
    }

    @Override
    public int compareTo(Status other) {
        return this.val - other.val;
    }
}

// 构造小顶堆
PriorityQueue<Status> queue = new PriorityQueue<>();

public ListNode mergeKLists(ListNode[] lists) {

    // lists = [[1,4,5],[1,3,4],[2,6]]
    // 此处的每个 node，其实是 lists 中链表数组的头指针
    for (ListNode node : lists) {
        // for loop：把 1, 1, 2 装入小顶堆，
        // 即将 lists 中每个链表数组中最小元素装入小顶堆
        if (node != null) {
            queue.offer(new Status(node.val, node));
        }
    }
    
    // 虚拟节点和尾指针 
    ListNode L = new ListNode(0);
    ListNode tail = L;

    while (!queue.isEmpty()) {
        // 弹出（小顶）堆的堆顶元素
        Status top = queue.poll();
        // 尾插法
        tail.next = top.ptr;
        tail = tail.next;
        
        // 如果弹出的 top 节点所属的链表还有剩余节点的情况下
        if (top.ptr.next != null) {
            // 将 top 下一个指向节点送入优先队列
            queue.offer(new Status(top.ptr.next.val, top.ptr.next));
        }
    }
    return L.next;
}

合并两个链表

1669. 合并两个链表

题目

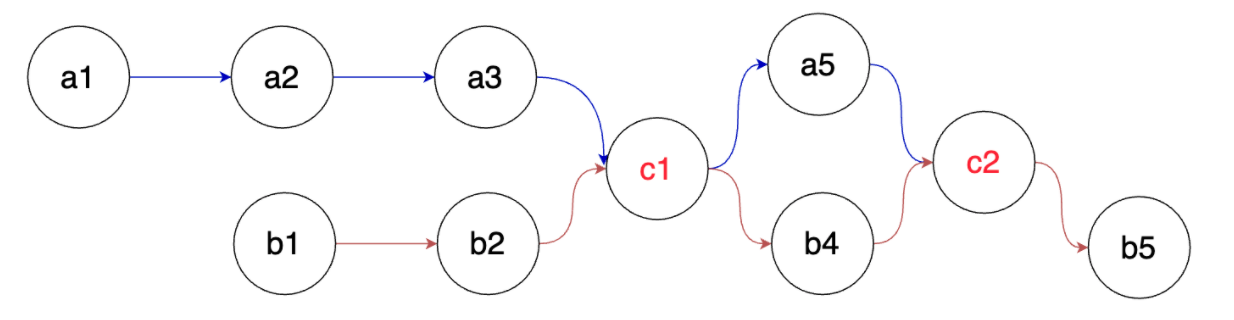
【LeetCode 1669】：给你两个链表 list1 和 list2 ，它们包含的元素分别为 n 个和 m 个。请你将 list1 中下标从 a 到 b 的全部节点都删除，并将list2 接在被删除节点的位置。

下图中蓝色边和节点展示了操作后的结果：

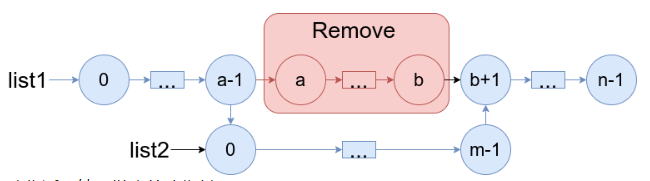
请你返回结果链表的头指针。

算法思想

1. 找到 list1 中第 a-1 个节点 preA，以及第 b+1 个节点 atfB
2. 由于 $1\le{a}\le{v}<{n-1}$，因此 preA 和 atfB 一定存在
3. 然后让 preA 的 next 指向 list2 的头节点，再让 list2 的尾节点的 next 指向 atfB 即可

public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {

    ListNode preA = list1;
    for (int i = 0; i < a - 1; i++) {
        preA = preA.next;
    }

    ListNode preB = preA;
    for (int i = 0; i < b - a + 2; i++) {
        preB = preB.next;
    }

    // concat
    preA.next = list2;

    while (list2.next != null) {
        list2 = list2.next;
    }
    list2.next = preB;

    return list1;
}

快慢指针专题

寻找中间节点

876. 链表的中间结点

题目

【LeetCode 876】：给你单链表的头结点 head ，请你找出并返回链表的中间结点。如果有两个中间结点，则返回第二个中间结点。

【推荐】快慢指针

算法思想

用两个指针 slow 与 fast 一起遍历链表。slow 一次走一步，fast 一次走两步。那么当 fast 到达链表的末尾时，slow 必然位于中间。

备注：如果有两个中间结点，则返回第 1 个中间结点，请参考 判断链表是否是回文序列#【推荐】使用快慢指针

// 不带虚拟节点
// 如果有两个中间结点，则返回第二个中间结点。
public ListNode middleNode(ListNode head) {

    ListNode slow = head, fast = head;

    while (fast != null && fast.next != null) {
        slow = slow.next;
        fast = fast.next.next;
    }
    return slow;
}

寻找倒数第 K 个元素

面试题 02.02. 返回倒数第 k 个节点

题目

【面试题 02.02.】：实现一种算法，找出单向链表中倒数第 k 个节点。返回该节点的值。

示例

input: list[1,2,3,4,5], k = 2
output: [4,5]

【推荐】快慢指针

算法思想

1. 快指针先移动 $k$ 步，然后慢指针再从头开始和快指针同时移动
2. 当快指针到链表末尾时，慢指针指向的节点即为目标节点
3. 特别注意链表长度小于 $k$ 情况，寻找 $k$ 位置时必须判断 fast 是否为 null

public int kthToLast(ListNode head, int k) {

    ListNode fast = head;
    ListNode slow = head;

    while (k > 0) { // 快指针先走 k 步
        fast = fast.next;
        k--;
    }
    if (fast == null) { // 说明链表长度不足 k
        return head.val;
    }
    // 快慢指针
    while (fast != null) {
        fast = fast.next;
        slow = slow.next;
    }
    return slow.val;
}

旋转链表

61. 旋转链表

题目

【LeetCode 61】：给你一个链表的头节点 head ，旋转链表，将链表每个节点向右移动 k 个位置。

【推荐】快慢指针

算法思想

使用双指针找到倒数 $k$ 的位置，然后拼接两个链表即可。比如 [1,2,3,4,5] 拆成 [1,2,3] 和 [4,5]，然后拼接两个链表

1. 已知链表长度 len，求 k=k%len

2. 如果 k==0 则无需旋转，否则进行下面操作

   • 快指针先走 $k$ 步，然后慢指针和快指针一起走
   • 快指针走到表尾时，慢指针所在位置即为拆分位置
   • 把快指针指向的节点连接至表头，然后慢指针执行断链操作
   • 最终返回新链表的头节点

   // 快慢指针
   public ListNode rotateRight(ListNode head, int k) {
   
       // base case
       if (head == null || k == 0) {
           return head;
       }
   
       int len = 0; 
       // H 记录 head 位置
       ListNode H = head;
       // 快指针
       ListNode fast = head;
       // 慢指针
       ListNode slow = head;
   
       while (head != null) {
           head = head.next;
           len++;
       } // 此情况下的 head 指向 null
       if (k % len == 0) {
           return H;
       }
   
       // 此时 fast 从头开始走 K 步
       // 要注意 K 超出 len 的部分，使用模运算抵消
       // len = 5 时，k = 2 和 7 一样效果
       while ((k % len) > 0) {
           k--;
           fast = fast.next;
       }
   
       // 在快指针走了 k 步后，快慢指针一起行动
       // 当 fast 走到最后一个节点（fast.next == null）时
       // slow 处于倒数 k 个节点的前驱
       while (fast.next != null) {
           fast = fast.next;
           slow = slow.next;
       }
       // 记录新链表头节点的位置
       ListNode L = slow.next;
       // 拆分链表
       slow.next = null;
       fast.next = H;
       
       return L;
   }

【推荐】构造循环链表

算法思想

记给定链表的长度为 n，注意到当向右移动的次数 $k≥n$ 时，我们仅需要向右移动 $k%n$ 次即可（每移动 n 次都会使链表变为原状），新链表的最后一个节点为原链表的第 (n-1)-(k%n) 个节点（从 0 开始计数）。我们可以先将给定的链表连接成环，然后将指定位置断开。

1. 首先计算链表长度 n，并找到链表的尾节点，将其与头节点相连，构造循环链表
2. 然后找到新链表的最后一个节点，将当前闭合尾环的链表断开即可
3. 特别注意，当链表不大于 1 或 k 为 n 的倍数时，新链表与原链表相同，不需要任何处理

public ListNode rotateRight(ListNode head, int k) {

    // base case
    if (k == 0 || head == null || head.next == null) {
        return head;
    }
    // 从 0 开始计数
    int len = 1;
    ListNode p = head;
    while (p.next != null) {
        p = p.next;
        len++;
    }
    // pos = (n - 1) - (k % n)
    // 新链表的最后一个节点为原链表的第 pos 个节点（从 0 开始计数）
    int count = len - k % len;
    if (count == len) {
        return head;
    }
    // 构造循环链表
    p.next = head;

    // 寻找新链表的尾节点位置
    while (count-- > 0) {
        p = p.next;
    }

    // 记录新链表的头节点位置
    ListNode L = p.next;
    // 将环断开
    p.next = null;
    
    return L;
}

删除链表元素专题

更多题目

LeetCode 19.删除链表的倒数第 N 个结点
LeetCode 82.删除排序链表中的重复元素 II
LeetCode 83.删除排序链表中的重复元素
LeetCode 203.移除链表元素
LeetCode 237.删除链表中的节点
LeetCode 1474.删除链表 M 个节点之后的 N 个节点

删除特定节点

203. 移除链表元素

题目

【LeetCode 203】：给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回 新的头节点 。

迭代删除

算法思想

1. 由于链表的头节点 head 有可能删除，因此创建虚拟节点 dummyNode，使其指向 head
2. 使用 cur 表示当前节点，如果 cur 的下一个节点不为空且下一个节点值等于给定的 val，则需要删除下一个节点
3. 如果 cur 的下一个节点值不等于给定的 val，则保留下一个节点，将 cur 移至下一个节点即可
4. 当 cur 的下一个节点为空时，链表遍历结束，此时所有节点值等于 val 的节点都被删除

public ListNode removeElements(ListNode head, int val) {
    
    ListNode dummyNode = new ListNode(0);
    dummyNode.next = head;
    ListNode cur = dummyNode;
    
    while (cur.next != null) {
        if (cur.next.val != val) {
            cur = cur.next;
        } else {
            cur.next = cur.next.next;
        }
    }
    return dummyNode.next;
}

递归删除

算法思想

1. 首先对除了头节点 head 以外的节点进行删除操作，然后判断 head 的节点值是否等于给定的 val。
2. 如果 head 的节点值等于 val，则 head 需要被删除，因此删除操作后的头节点为 head.next
3. 如果 head 的节点值不等于 val，则 head 保留，因此删除操作后的头节点还是 head。

上述过程是一个递归的过程。递归的终止条件是 head 为空，此时直接返回 head。当 head 不为空时，递归地进行删除操作，然后判断 head 的节点值是否等于 val 并决定是否要删除 head。

// 递归删除
public ListNode removeElements(ListNode head, int val) {
    // base case
    if (head == null) {
        return head;
    }
    head.next = removeElements(head.next,val);
    return head.val == val ? head.next : head;
}

删除倒数第 n 个节点

19. 删除链表的倒数第 N 个结点

题目

【LeetCode 19】：给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

【进阶】：使用一趟扫描实现算法？

计算链表长度（节点编号从 1 开始）

算法思想

1. 首先从头节点开始遍历链表获取长度 L
2. 然后再次从头节点遍历链表，当遍历到第 L-n+1 个节点时，就是我们要找的节点

为方便删除操作，可以从虚拟节点开始遍历 L-n+1 个节点。当遍历到第 L-n+1 个节点时，它的下一个节点就是我们要删除的节点：

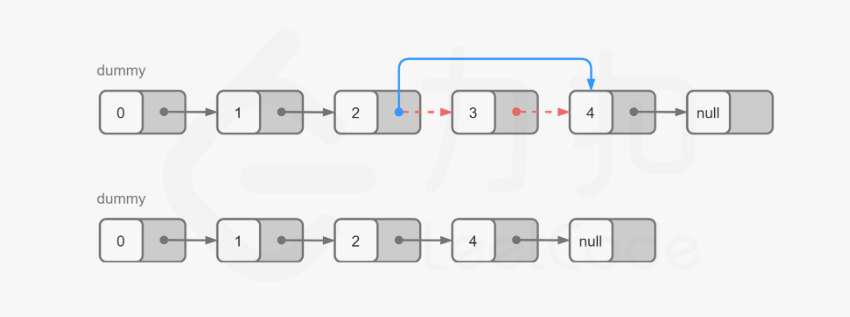
public ListNode removeNthFromEnd(ListNode head, int n) {

    ListNode dummyNode = new ListNode(0);
    dummyNode.next = head;

    int len = getLength(head);
    ListNode cur = dummyNode;

    for (int i = 1; i < len - n + 1; i++) {
        cur = cur.next;
    }
    cur.next = cur.next.next;
    ListNode ans = dummyNode.next;
    return ans;
}
public int getLength(ListNode head) {
    int length = 0;
    while (head != null) {
        ++length;
        head = head.next;
    }
    return length;
}

栈

算法思想

1. 在遍历链表时将所有节点入栈
2. 根据栈「先进后出」的原则，我们弹出栈的第 n 个节点就是需要删除的节点，并且目前栈顶的节点就是待删除节点的前驱节点。

public ListNode removeNthFromEnd(ListNode head, int n) {

    ListNode dummyNode = new ListNode(0);
    dummyNode.next = head;
    Deque<ListNode> stack = new LinkedList<>();
    ListNode cur = dummyNode;
    
    // 链表节点全部入栈
    while (cur != null) {
        stack.push(cur);
        cur  = cur.next;
    }
    
    for (int i = 0; i < n; i++) {
        stack.pop();
    }
    // 记录待删除节点的前驱
    ListNode prev = stack.peek();
    prev.next = prev.next.next;
    
    return dummyNode.next;
}

【推荐】快慢指针

算法思想

1. 由于要找到倒数第 n 个节点，可以使用快慢指针
2. 先使用快指针走 n 步，此时快慢指针之间相隔 n-1 个节点，即快指针比慢指针超前 n 步
3. 此后，同时使用快慢指针遍历链表，当快指针遍历到表尾（快指针为 null）时，慢指针恰好指向倒数第 n 个节点

由于得到倒数等 n 节点的前驱节点更利于删除操作，我们可以初始时将慢指针指向虚拟节点 dummyNode，这样一来，当快指针遍历到链表末尾时，慢指针的下一个节点就是待删除的节点

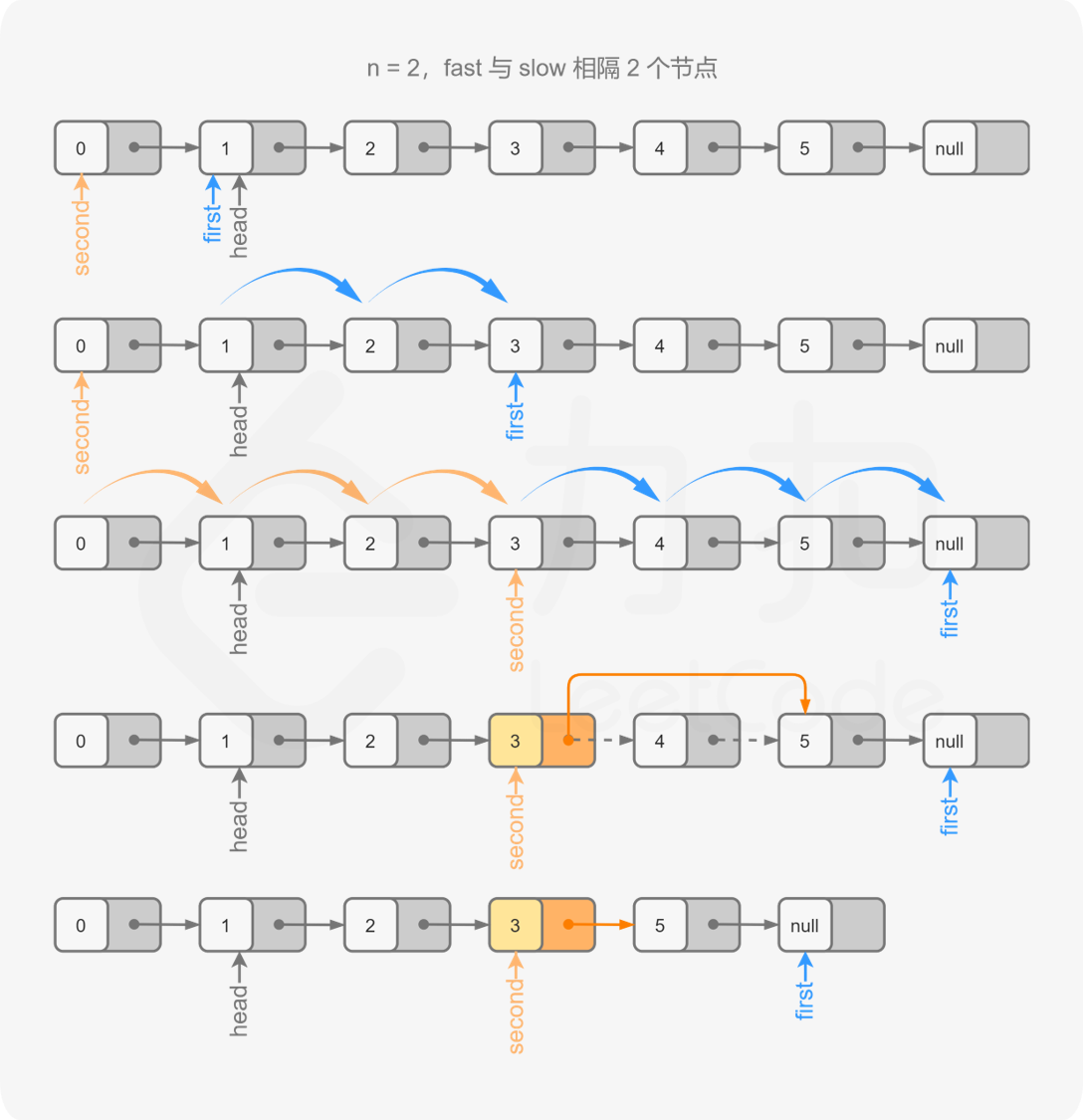
public ListNode removeNthFromEnd(ListNode head, int n) {
    
    ListNode dummyNode = new ListNode(0);
    dummyNode.next = head;

    ListNode fast = head;
    // 特殊情况，要落在倒数 k 个节点的前驱
    ListNode slow = dummyNode; 
    
    while (n > 0) { // 快指针先走 n 步
        n--;
        fast = fast.next;
    }
    while (fast != null) {
        fast = fast.next;
        slow = slow.next;
    }
    // 找到待删除节点的前驱后删除目标节点
    slow.next = slow.next.next;
    
    return dummyNode.next; 
}

删除重复元素

重复元素只保留一个

83. 删除排序链表中的重复元素

题目

【LeetCode 83】：给定一个已排序的链表的头 head ， 删除所有重复的元素，使每个元素只出现一次 。返回 已排序的链表 。

算法思想

由于给定的链表是排好序的，因此重复的元素在链表中出现的位置是连续的，因此我们只需要对链表进行一次遍历，就可以删除重复的元素。

1. 指针 cur 从表头开始遍历
2. 当前 cur 与 cur.next 对应的元素相同，则将 cur.next 从链表中移除
3. 否则说明链表中不存在其他与 cur 对应的元素相同的节点，可以将 cur 指向 cur.next
4. 当遍历完整个链表后，返回链表的头节点即可，但当我们遍历到链表最后一个节点时，cur.next 为空，如果不判断会报错。因此只需要遍历到链表的最后一个节点，不需要遍历完整个链表
5. 特别注意，单链表删除操作一般定位前驱删除后继，因此本策略选择删除 cur.next

public ListNode deleteDuplicates(ListNode head) {

    // base case
    if (head == null) {
        return head;
    }
    ListNode cur = head;

    while (cur.next != null) {
        if (cur.val == cur.next.val) {
            cur.next = cur.next.next;
        } else {
            cur = cur.next;
        }
    }
    return head;
}

重复元素都不要

82. 删除排序链表中的重复元素 II

题目

【LeetCode 82】：给定一个已排序的链表的头 head ， 删除原始链表中所有重复数字的节点，只留下不同的数字 。返回 已排序的链表 。

算法思想

由于给定的链表是排好序的，因此重复的元素在链表中出现的位置是连续的，因此我们只需要对链表进行一次遍历，就可以删除重复的元素。由于链表的头节点可能会被删除，因此我们需要额外使用一个哑节点（dummy node）指向链表的头节点。

1. 指针 cur 指向虚拟节点，开始遍历链表
2. 如果当前 cur.next 与 cur.next.next 对应的元素相同，就需要将 cur.next 以及所有后面拥有相同元素值的链表节点全部删除
3. 记录下元素值 x ，随后不断将 cur.next 从链表中移除，直到 cur.next 为空或者元素值不为 x 为止，此时链表所有元素值为 x 的节点全部删除
4. 如果当前 cur.next 与 cur.next.next 对应的元素不相同，那么说明链表中只有一个元素值为 cur.next 的节点，直接将 cur 指向 cur.next
5. 当遍历完整个链表之后，我们返回链表的的哑节点的下一个节点 dummy.next 即可。
6. 特别注意，cur.next 以及 cur.next.next 可能为空节点，如果不加以判断，可能会产生运行错误。

public ListNode deleteDuplicates(ListNode head) {

    // base case
    if (head == null) {
        return head;
    }

    ListNode dummyNode = new ListNode(0);
    dummyNode.next = head;

    ListNode cur = dummyNode;

    while (cur.next != null && cur.next.next != null) {
        if (cur.next.next.val == cur.next.val) {
            int x = cur.next.val;
            // delete all duplicates
            while (cur.next != null && cur.next.val == x) {
                cur.next = cur.next.next;
            }
        } else {
            cur = cur.next;
        }
    }

    return dummyNode.next;

}

链表专题Ⅰ—环问题与双链表设计

内容概览

题目	说明
环形链表	中等
双链表设计	中等

链表环问题

142. 环形链表 II

参考资料

链表8.又难又简单的链表环的问题

问题

【LeetCode 142】：给定一个链表的头节点 head，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

【推荐】哈希

算法思想

遍历链表中的每个节点，并将其记录下来；一旦遇到此前遍历过的节点，就可以判断链表中存在环。

public ListNode detectCycle(ListNode head) {
    ListNode pos = head;

    Set<ListNode> visited = new HashSet<>();

    while (pos != null) {
        if (visited.contains(pos)) {
            return pos; // 入环口
        } else {
            visited.add(pos);
        }
        pos = pos.next;
    }
    return null;
}

【推荐】快慢指针

算法思想

• 借助快慢指针 fast 和 slow，两只正初始位于链表的头部。随后，慢指针每次向后移动一个位置，快指针向后移动两个位置
• 如果链表存在环，则快指针最终将再次与慢指针在环中相遇

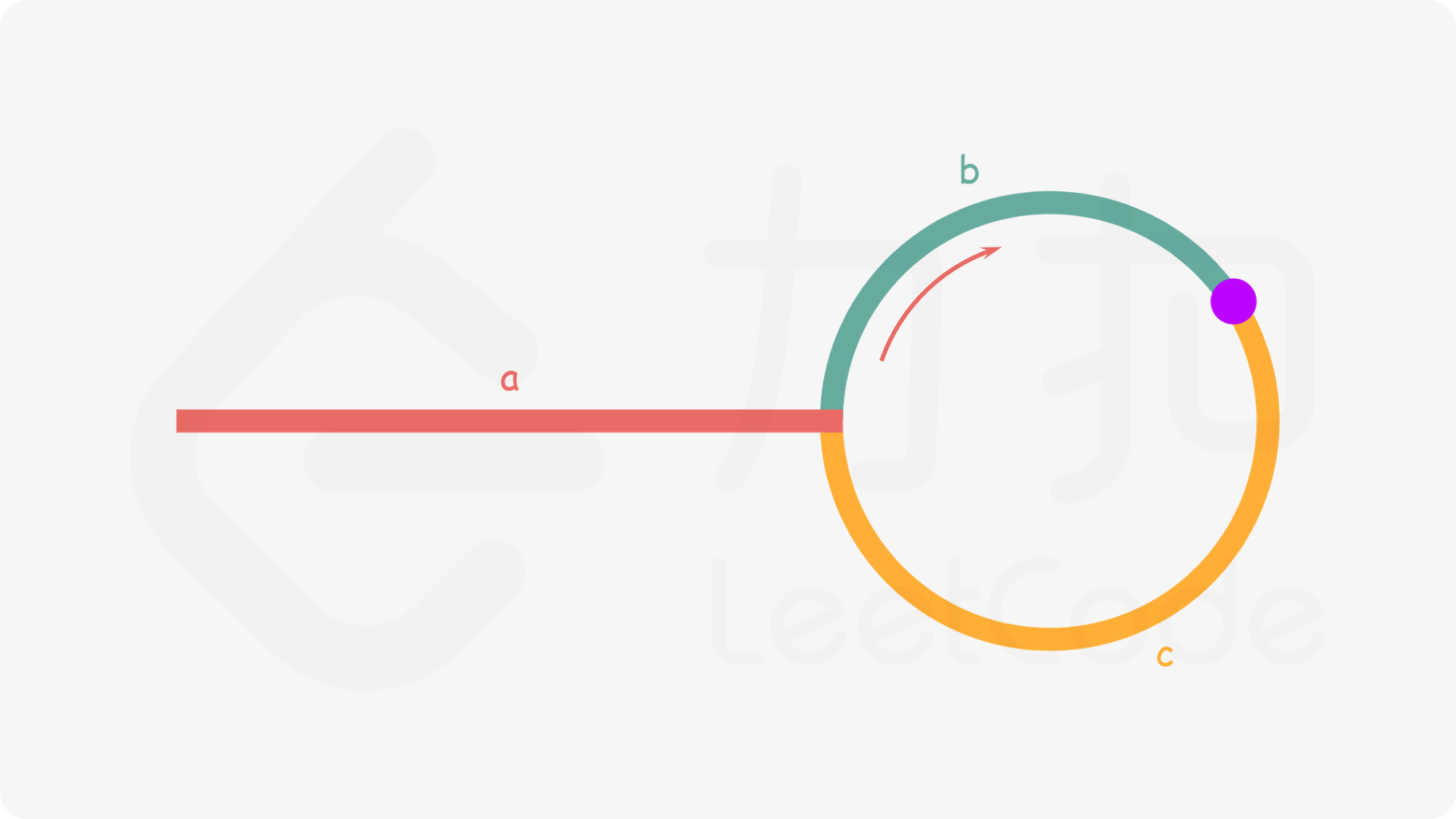
假设链表中环外部分的长度为 $a$，慢指针进入环后，又走了 $b$ 的距离与快指针相遇。此时快指针已经走完环的 $n$ 圈，因此它走过的总距离为 $a+n(b+c)+b=a+(n+1)b+nc$。
根据题意，任意时刻，快指针走过的距离都是慢指针的 $2$ 倍，因此，有如下式子：

$$a+(n+1)b+nc=2(a+b)⟹a=c+(n−1)(b+c)$$

有了 $a=c+(n−1)(b+c)$ 的等量关系，我们发现：从相遇点到入环点的距离加上 $n-1$ 圈的环长，恰好等于从链表头部到入环点的距离。

因此，当发现快慢指针相遇时再额外使用一个指针 ptr 。起始，它指向链表头部；随后，它和慢指针每次向后移动一个位置。最终，它们会在入环点相遇。

public ListNode detectCycle(ListNode head) {
    
    if (head == null) {
        return null;
    }
    ListNode slow = head, fast = head;
    
    while (fast != null) {
        // 慢指针每次走一步
        slow = slow.next;
        // 快指针每次走两步
        if (fast.next != null) {
            fast = fast.next.next;
        } else { // 如果快指针提前走完
            return null; // 说明无环
        }
        // 入环口判断
        if (fast == slow) { // 如果快慢指针相遇，说明存在环
            ListNode ptr = head;
            while (ptr != slow) {
                ptr = ptr.next;
                slow = slow.next;
            }
            // 返回入环口
            return ptr;
        }
    }
    return null;
}

双向链表设计

参考资料

链表7：应用甚广的双向链表

LeetCode 707.设计链表