算法通关 3 - 数组专题

数组专题—数组基础

内容概览

题目	说明
在数组首部、中间和尾部插入元素	简单
在数组首部、中间和尾部删除元素	简单
单调数列	中等
搜索插入位置	困难
合并两个有序数组	简单

参考资料

常见数据结构1.别说你懂数组-这些问题经常翻车

数组基本操作

数组创建和初始化

int[] arr = new int[10];

int[] arr = new int[] {0,1,2,3,4};

int[] arr = {0,1,2,3,4};

查找元素

/**
 * 查找元素
 * 
 * @param size 已经存放的元素个数
 * @param key 待查找的元素 
 */
public int find(int[] arr, int size, int key) {

    for (int i = 0; i < size; i++) {
        if (arr[i] == key) {
            return i;
        }
    }
    return -1;
}

增加元素

/**
 * 将给定的元素插入到有序数组的对应位置中
 * 
 * @param size 已经存放的元素个数
 * @param e 待插入的元素 
 */
public int insert(int[] arr, int size, int e) {

    if (size >= arr.length) {
        return -1;
    }

    int index = size;
    // 寻找新元素的插入位置
    for (int i = 0; i < size; i++) {
        if (e < arr[i]) {
            index = i;
            break;
        }
    }
    // 元素后移
    for (int j = size; j > index; j--) {
        arr[j] = arr[j -1]; // index 下标开始的元素后移一个位置
    }
    // 插入数据
    arr[index] = e;
    return index;
}

删除元素

/**
 * 删除元素
 * 
 * @param size 已经存放的元素个数
 * @param key 待删除的元素 
 */
public int delete(int[] arr, int size, int key) {
    
    int index = -1;
    // 找到待删除元素的位置
    for (int i = 0; i < size; i++) {
        if (arr[i] == key) {
            index = i;
            break;
        }
    }
    if (index != -1) {
        for (int i = index + 1; i < size; i++) {
            arr[i - 1] = arr[i];
        }
        size--;
    }
    return size;
}

单调数组专题

单调数列

896. 单调数列

【LeetCode 896】：如果数组是单调递增或单调递减的，那么它是 单调 的。

如果对于所有 i <= j，nums[i] <= nums[j]，那么数组 nums 是单调递增的。 如果对于所有 i <= j，nums[i]> = nums[j]，那么数组 nums 是单调递减的。

当给定的数组 nums 是单调数组时返回 true，否则返回 false。

两次遍历：

遍历两次数组，分别判断是否单调递增或单调递减。

// 两次遍历
public boolean isMonotonic(int[] nums) {
    return isSorted(nums, true) || isSorted(nums, false);
}

private boolean isSorted(int[] nums, boolean increasing) {

    if (increasing) { // 判断单调增
        for (int i = 0; i < nums.length - 1; i++) {
            if (nums[i] > nums[i + 1]) {
                return false;
            }
        }
    } else { // 判断单调减
        for (int i = 0; i < nums.length - 1; i++) {
            if (nums[i] < nums[i + 1]) {
                return false;
            }
        }
    }
    // 不满足上述失败情况，则符合要求
    return true;
}

一次遍历：

遍历数组 nums，若既遇到了 nums[i]>nums[i+1] 又遇到了 nums[i′]<nums[i′+1]，则说明 nums 既不是单调递增的，也不是单调递减的。

public boolean isMonotonic(int[] nums) {

    boolean inc = true, dec = true;

    for (int i = 0; i < nums.length - 1; i++) {
        
        if (nums[i] > nums[i + 1]) {
            inc = false;
        }
        if (nums[i] < nums[i +1]) {
            dec = false;
        }
    }
    return inc || dec;
}

搜索插入位置

35. 搜索插入位置

【LeetCode 35】：给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 $O(log⁡n)$ 的算法。

输入: nums = [1,3,5,6], target = 5
输出: 2

输入: nums = [1,3,5,6], target = 2
输出: 1

输入: nums = [1,3,5,6], target = 7
输出: 4

二分查找：假设题意是叫你在排序数组中寻找是否存在一个目标值，那么训练有素的读者肯定立马就能想到利用二分法在 $O(log⁡n)$ 的时间内找到是否存在目标值。
但这题还多了个额外的条件，即如果不存在数组中的时候需要返回按顺序插入的位置，那我们还能用二分法么？答案是可以的，我们只需要稍作修改即可。

考虑这个插入的位置 pos，它成立的条件为：nums[pos−1]<target≤nums[pos]

其中 nums 代表排序数组。由于如果存在这个目标值，我们返回的索引也是 pos，因此我们可以将两个条件合并得出最后的目标：「在一个有序数组中找第一个大于等于 target 的下标」。

【推荐】二分查找

问题转化到这里，直接套用二分法即可，即不断用二分法逼近查找第一个大于等于 target 的下标，下文给出的代码是笔者习惯的二分写法，ans 初值设置为数组长度可以省略边界条件的判断，因为存在一种情况是 target 大于数组中的所有数，此时需要插入到数组长度的位置。

public int searchInsert(int[] nums, int target) {

    int left = 0, right = nums.length - 1, ans = nums.length;

    while (left <= right) {

        int mid = left + ((right - left) >> 1);
        if (target <= nums[mid]) {
            ans = mid;
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return ans;
}

合并两个有序数组

88. 合并两个有序数组

问题

【LeetCode 88】：给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

【基础】双指针

归并排序思想，借助双指针，每次从两个数组头部取出比较小的数字放到结果中。弊端是空间复杂度 $O(N)$

public void merge(int[] nums1, int m, int[] nums2, int n) {
    int p1 = 0, p2 = 0;
    int[] sorted = new int[m + n];
    int cur;
    while (p1 < m || p2 < n) {
        if (p1 == m) {
            cur = nums2[p2++];
        } else if (p2 == n) {
            cur = nums1[p1++];
        } else if (nums1[p1] < nums2[p2]) {
            cur = nums1[p1++];
        } else {
            cur = nums2[p2++];
        }
        sorted[p1 + p2 - 1] = cur;
    }
    for (int i = 0; i != m + n; ++i) {
        nums1[i] = sorted[i];
    }
}

【推荐】逆向双指针

思路 1 需要开辟临时空间，如果直接合并到数组 nums1，其中的元素可能会在取出之前被覆盖。由于 nums1 的后半部分是空的，因此可以考虑直接覆盖而不会影响结果。我们可以指针设置为从后向前遍历，每次取两者之中的较大者放进 nums1 的最后面

public void merge(int[] nums1, int m, int[] nums2, int n) {

    int p1 = m - 1, p2 = n - 1;
    int tail = m + n - 1;
    int curr;

    while (p1 >= 0 || p2 >= 0) {

        if (p1 == -1) { // p1 到头
            curr = nums2[p2--];
        } else if (p2 == -1) { // p2 到头
            curr = nums1[p1--];
        } else if (nums1[p1] >= nums2[p2]) {
            curr = nums1[p1--];
        } else {
            curr = nums2[p2--];
        }
        nums1[tail--] = curr;
    }
}

数组专题—双指针思想

内容概览

题目	说明
原地移除所有数值等于 val 的元素	通关
删除有序数组中的重复项	通关
奇偶元素移动问题	通关
数组汇总区间问题	通关
数组缺失区间问题	通关
字符串替换问题	通关

参考资料

简单好用的双指针思想

双指针类型

• 快慢型指针：一个在前面走，一个在后面走
• 对撞型指针：从两端向中间走
• 背向型指针：从中间向两端走

删除元素专题

原地移除所有数值等于 val 的元素

27. 移除元素

问题

【LeetCode 27】：给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

不要使用额外的数组空间，你必须仅使用 $O(1)$ 额外空间并 原地 修改输入数组。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

【推荐】快慢型双指针

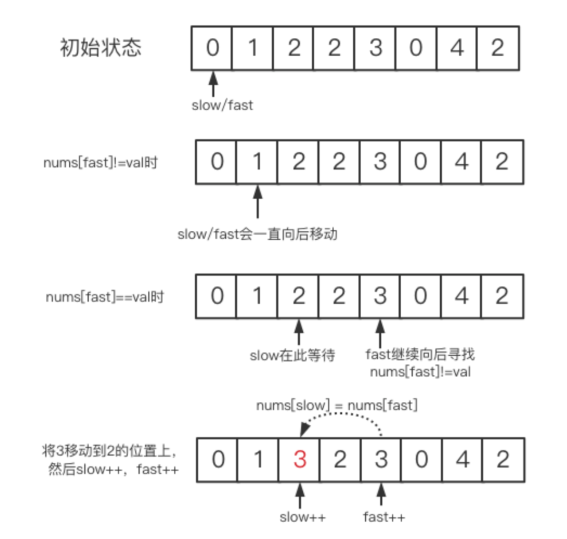
由于题目要求删除数组中等于 val 的元素，因此输出数组的长度一定小于等于输入数组的长度，我们可以把输出的数组直接写在输入数组上。可以使用双指针：快指针 fast 指向当前要处理的元素，慢指针 slow 指向有效部分。

• 如果快指针指向的元素不等于 val，则它一定是输出数组的元素，此时就将快指针指向的元素复制到慢指针指向的有效位置，然后双指针同时右移一位

• 如果快指针指向的元素等于 val，则它不能在输出数组中，此时慢指针指向的有效位置先按兵不动，快指针右移一位

整个过程保持不变的性质是：区间 [0,slow) 中的元素都不等于 val。当左右指针遍历完输入数组以后，slow 的值就是输出数组的长度。

这样的算法在最坏情况下（输入数组中没有元素等于 val），左右指针各遍历了数组一次。

public int removeElement(int[] nums, int val) {

    int slow = 0;
    for (int fast = 0; fast < nums.length; ++fast) {

        if (nums[fast] != val) {
            nums[slow++] = nums[fast];
        }
    }

    return slow;
}

对撞型双指针

如果要移除的元素恰好在数组的开头，例如序列 [1,2,3,4,5]，当 val 为 1 时，我们需要把每一个元素都左移一位。注意到题目中说：「元素的顺序可以改变」。实际上我们可以直接将最后一个元素 5 移动到序列开头，取代元素 1，得到序列 [5,2,3,4]，同样满足题目要求。这个优化在序列中 val 元素的数量较少时非常有效。
实现方面，我们依然使用双指针，两个指针初始时分别位于数组的首尾，向中间移动遍历该序列。

• 如果左指针 left 指向的元素等于 val，此时将右指针 right 指向的元素复制到左指针 left 的位置，然后右指针 right 左移一位。
• 如果赋值过来的元素恰好也等于 val，可以继续把右指针 right 指向的元素的值赋值过来（左指针 left 指向的等于 val 的元素的位置继续被覆盖），直到左指针指向的元素的值不等于 val 为止。
  当左指针 left 和右指针 right 重合的时候，左右指针遍历完数组中所有的元素。

这样的方法两个指针在最坏的情况下合起来只遍历了数组一次。与方法一不同的是，方法二避免了需要保留的元素的重复赋值操作。

以 nums=[0,1,2,2,3,0,4,2]，val=2 为例，当 left == riht 时，left 及其左侧即为所求。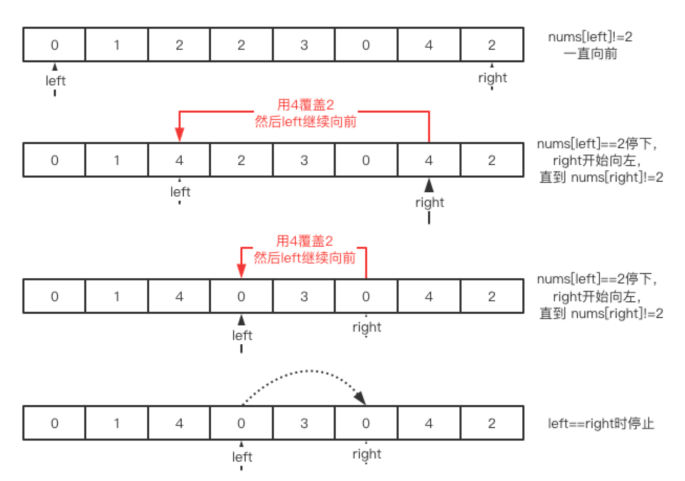

public int removeElement(int[] nums, int val) {

    int left = 0;
    int right = nums.length - 1;

    while (left <= right) {
        if (nums[left] == val) {
            nums[left] = nums[right--];
        } else {
            left++;
        }
    }
    return left;
}

删除有序数组中的重复项

26. 删除有序数组中的重复项

问题

【LeetCode 26】：给你一个 非严格递增排列 的数组 nums ，请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。

考虑 nums 的唯一元素的数量为 k ，你需要做以下事情确保你的题解可以被通过：

• 更改数组 nums ，使 nums 的前 k 个元素包含唯一元素，并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
• 返回 k 。

【推荐】快慢型双指针

由于给定的数组 nums 是有序的，因此对于任意 $i<j$，如果 nums[i]=nums[j]，则对任意 $i≤k≤j$，必有 nums[i]=nums[k]=nums[j]，即相等的元素在数组中的下标一定是连续的。利用数组有序的特点，可以通过双指针的方法删除重复元素。

• 如果数组 nums 的长度为 0，则数组不包含任何元素，因此返回 0。
• 当数组 nums 的长度大于 0 时，数组中至少包含一个元素，在删除重复元素之后也至少剩下一个元素，因此 nums[0] 保持原状即可，从下标 1 开始删除重复元素。

定义两个指针 fast 和 slow 分别为快指针和慢指针，快指针表示遍历数组到达的下标位置，慢指针表示下一个不同元素要填入的下标位置，初始时两个指针都指向下标 1。

假设数组 nums 的长度为 $n$。将快指针 fast 依次遍历从 $1$ 到 $n−1$ 的每个位置，对于每个位置，如果 nums[fast]≠nums[fast−1]，说明 nums[fast] 和之前的元素都不同，因此将 nums[fast] 的值复制到 nums[slow]，然后将 slow 的值加 1，即指向下一个位置。

遍历结束之后，从 nums[0] 到 nums[slow−1] 的每个元素都不相同且包含原数组中的每个不同的元素，因此新的长度即为 slow，返回 slow 即可

public int removeDuplicates(int[] nums) {
    
    if (nums.length == 0) {
        return 0;
    }
    
    int fast = 1, slow = 1;
    while (fast < nums.length) {
        
        if (nums[fast] != nums[fast - 1]) {
            nums[slow] = nums[fast];
            ++slow;
        }
        ++fast;
    }
    return slow;
}

奇偶元素移动专题

问题

【LeetCode 905】：给你一个整数数组 nums，将 nums 中的的所有偶数元素移动到数组的前面，后跟所有奇数元素。

返回满足此条件的 任一数组 作为答案。

对撞型双指针 + 原地交换

1. 先从 nums 左侧开始遍历，如果遇到的是偶数，就表示这个元素已经排好序了，继续从左往右遍历，直到遇到一个奇数。
2. 然后从 nums 右侧开始遍历，如果遇到的是奇数，就表示这个元素已经排好序了，继续从右往左遍历，直到遇到一个偶数。
3. 交换这个奇数和偶数的位置，并且重复两边的遍历，直到在中间相遇，nums 排序完毕。

public int[] sortArrayByParity(int[] nums) {

    int left = 0, right = nums.length -1;
    while (left < right) {
        // 如果遇到的是偶数，就表示这个元素已经排好序了，继续从左往右遍历，直到遇到一个奇数。
        while (left < right && nums[left] % 2 == 0) {
            left++;
        }
        // 如果遇到的是奇数，就表示这个元素已经排好序了，继续从右往左遍历，直到遇到一个偶数。
        while (left < right && nums[right] % 2 == 1) {
            right--;
        }
        // 交换这个奇数和偶数的位置，并且重复两边的遍历，直到在中间相遇
        if (left < right) {
            int temp = nums[left];
            nums[left] = nums[right];
            nums[right] = temp;
            left++;
            right--;
        }
    }
    return nums;
}

对撞型指针 + 遍历

新建数组 res 用来保存排完序的数组。遍历一遍 nums，遇到偶数则从 res 左侧开始替换元素，遇到奇数则从 res 右侧开始替换元素。遍历完成后，res 就保存了排序完毕的数组。

public int[] sortArrayByParity(int[] nums) {

    int [] res = new int[nums.length];
    int left = 0, right = nums.length -1;

    for (int num : nums) {
        if (num % 2 == 0) { // 偶数
            res[left++] = num;
        } else { // 奇数
            res[right--] = num; 
        }
    }
    return res;
}

数组轮转问题

问题

【LeetCode 189】：给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

数组反转

以 $n=7$，$k=3$ 为例：

操作	结果
原始数组	1 2 3 4 5 6 7
翻转所有元素	7 6 5 4 3 2 1
翻转 $[0,k mod n−1]$ 区间的元素	5 6 7 4 3 2 1
翻转 $[k mod n,n−1]$ 区间的元素	5 6 7 1 2 3 4

public void rotate(int[] nums, int k) {

    k %= nums.length;

    reverse(nums, 0, nums.length - 1);
    reverse(nums, 0, k - 1);
    reverse(nums, k, nums.length - 1);

}

public void reverse(int[] nums, int begin, int end) {

    while (begin < end) {
        int temp = nums[begin];
        nums[begin] = nums[end];
        nums[end] = temp;
        begin++;
        end--;
    }
}

数组区间专题

汇总区间

问题

【LeetCode 228】：给定一个 无重复元素 的 有序 整数数组 nums 。

返回 恰好覆盖数组中所有数字 的 最小有序 区间范围列表 。也就是说，nums 的每个元素都恰好被某个区间范围所覆盖，并且不存在属于某个范围但不属于 nums 的数字 x 。

列表中的每个区间范围 [a,b] 应该按如下格式输出：

• "a->b" ，如果 a != b
• "a" ，如果 a == b

一次遍历

数组的位置 0 出发，向右遍历。每次遇到相邻元素之间的差值大于 1 时，我们就找到了一个区间。遍历完数组之后，就能得到一系列的区间的列表。

在遍历过程中，维护下标 low 和 high 分别记录区间的起点和终点，对于任何区间都有 low≤high。当得到一个区间时，根据 low 和 high 的值生成区间的字符串表示。

• 当 low<high 时，区间的字符串表示为 "low→high"
• 当 low=high 时，区间的字符串表示为 "low"

public List<String> summaryRanges(int[] nums) {

    List<String> res = new ArrayList<>();
    int curr = 0;
    while (curr < nums.length) {
        int low = curr;
        curr++;
        while (curr < nums.length && nums[curr] == nums[curr - 1] + 1) {
            curr++;
        } // 寻找连续序列
        int high = curr - 1;
        StringBuilder temp = new StringBuilder(Integer.toString(nums[low]));
        if (low < high) {
            temp.append("->");
            temp.append(Integer.toString(nums[high]));
        }
        res.add(temp.toString());
    }
    return res;
}

快慢指针

1. 慢指针指向每个区间起始位置，快指针从慢指针位置开始向后遍历直达不满足连续递增（或者快指针到达数组边界），则确定当前区间；
2. 然后将 slow 更新为 fast + 1，作为下一个区间的起始位置，快指针继续如此循环

public List<String> summaryRanges(int[] nums) {

    List<String> res = new ArrayList<>();
    int slow = 0, fast = 0;

    while (fast < nums.length) {
        if (fast + 1 == nums.length || nums[fast] + 1 != nums[fast + 1]) {
            StringBuilder temp = new StringBuilder(Integer.toString(nums[slow]));
            if (slow != fast) {
                temp.append("->").append(Integer.toString(nums[fast]));
            }
            res.add(temp.toString());
            // 更新为下一个区间起始位置
            slow = fast + 1;
        }
        fast++;
    }
    return res;
}

缺失的区间

问题

【LeetCode 163】：给定一个排序的整数数组 nums ，其中元素的范围在闭区间 [lower, upper] 当中，返回不包含在数组中的缺失区间。

输入: nums = [0, 1, 3, 50, 75], lower = 0 和 upper = 99,
输出: [“2”, “4->49”, “51->74”, “76->99”]

遍历数组：

• （虚拟元素）在数组末尾添加一个额外的元素，简化处理最后一个区间的情况，该元素的值设为 upper + 1。
• 初始化变量 prev 为 lower - 1。这个变量用于跟踪上一个处理过的元素。

识别缺失的区间：

对数组中的每个元素进行遍历：

• 如果当前元素（num）恰好比 prev 大 1，说明它们之间没有缺失的区间，直接继续下一个元素。
• 如果当前元素大于 prev + 1，说明存在缺失的区间，将缺失的区间添加到 result 列表中。
• 更新 prev 为当前元素的值

处理最后一个区间：
检查 upper 是否大于 prev + 1：

• 如果是，说明在 prev + 1 和 upper 之间存在缺失的区间，将该区间添加到 result 列表中。
• 如果 upper 等于 prev + 1，将单个缺失的数字 upper 添加到 result 列表中。

public List<String> findMissingRanges(int[] nums, int lower, int upper) {

    List<String> result = new ArrayList<>();
    // 初始化 `prev` 为 `lower - 1`，用于跟踪上一个处理过的元素
    long prev = (long) lower - 1;  // 使用 long 类型避免整数溢出问题

    for (int num : nums) {
        // 若当前元素（`num`）恰好比 `prev` 大 1，说明它们之间没有缺失的区间，直接继续下一个元素（连续序列）

        // 若当前元素（`num`）恰好比 `prev` 大 2，说明它们之间缺失一个序列（缺失单个序列）
        if (num == prev + 2) {
            result.add(String.valueOf(prev + 1));
        } else if (num > prev + 2) {
            // 若两者相差超过 2，说明它们之间缺失连续序列（缺失若干序列）
            result.add((prev + 1) + "->" + (num - 1));
        }
        prev = num;
    }

    // 检查最后一个区间
    if (upper > prev + 1) {
        // `prev + 1` 和 `upper` 之间存在缺失的区间
        result.add((prev + 1) + "->" + upper);
    } else if (upper == prev + 1) {
        // 将单个缺失的数字 `upper` 添加到 `result` 列表中
        result.add(String.valueOf(upper));
    }
    return result;
}

字符串替换问题

问题

【剑指 Offer】：请实现一个函数，将一个字符串中的每个空格替换成 “%20”

输入：s = "We Are Happy";
输出：s = "We%20Are%20Happy";

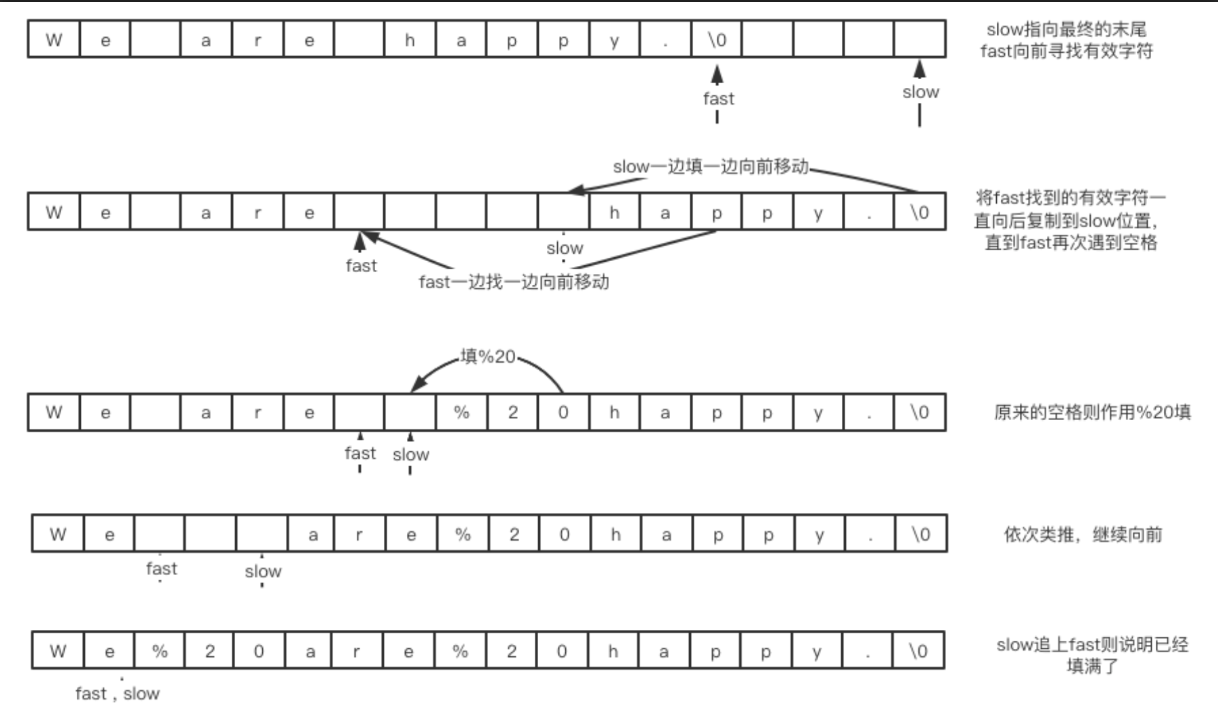
1. 遍历字符串，统计字符串中空格的总数 count，计算替换后的字符串长度，假设新字符串长度为 newLen，旧字符串长度为 oldLen，则 newLen = oldLen + 2 * count。
2. 从字符串的尾部开始复制和替换，快慢指针分别指向旧字符串和新字符串的末尾，慢指针不移动，快指针向前移动
3. 若快指针指向的不是空格，则将其复制到慢指针位置，然后快慢指针同时向前移动 1 步长
4. 若快指针指向的是空格，则在慢指针位置插入 %20，快指针向前移动 1 步长

public String replaceSpace(StringBuffer str) {

    if (str == null) {
        return null;
    }
    // count 统计空格数量
    int count = 0;
    // 旧字符串长度
    int oldLen = str.length();
    // 统计空格数量
    for (int i = 0; i < oldLen; i++) {
        if (str.charAt(i) == ' ') {
            count++;
        }
    }
    // 新字符串长度
    int newLen = oldLen + count * 2;
    str.setLength(newLen);
    // 快指针指向旧字符串末尾
    int fast = oldLen - 1;
    // 慢指针指向新字符串末尾
    int slow = newLen - 1;

    while (fast >= 0 && slow > fast) {
        char ch = str.charAt(fast);
        if (ch == ' ') {
            fast--;
            str.setCharAt(slow--, '0');
            str.setCharAt(slow--, '2');
            str.setCharAt(slow--, '%');
        } else { // 若快指针指向的不是空格，则将其复制到慢指针位置，然后快慢指针同时向前移动 1 步长
            str.setCharAt(slow, ch);
            fast--;
            slow--;
        }
    }
    return str.toString();
}

数组专题—数组强化

通关进度

题目	说明
数组出现次数超过一半的数字	通关
数组中只出现一次的数字	通关
荷兰旗问题	通关

数组出现次数超过一半的数字

问题

【剑指 Offer】：找出数组中出现次数超过一半的数字

思路

• 方法 1：排序统计
• 方法 2：哈希统计
• 方法 3：摩尔投票算法

哈希统计

public int majorityElement(int[] arr) {
    
    if (arr == null) {
        return 0;
    }
    Map<Integer, Integer> ans = new HashMap<>();
    for (int i = 0; i < arr.length; i++) {
        ans.put(arr[i], ans.getOrDefault(arr[i], 0) + 1);
        if (ans.get(arr[i]) > arr.length / 2) {
            return arr[i];
        }
    }
    return 0;
}

摩尔投票

• 如果一个数字出现的次数超过数组长度的一半，那么它出现的次数比其他所有数字出现次数的和还要多
• 遍历数组时，使用两个变量来保存当前候选数字和其对应的出现次数
• 如果遍历到的数字与候选数字相同，则增加计数，否则减少计数
• 当计数变为 0 时，更换候选数字，而最终的候选数字就是数组中出现次数超过一半的数字

public int majorityElement(int[] nums) {

    int candidate = 0;
    int count = 0;

    for (int num : nums) {
        if (count == 0) {
            candidate = num;
        }

        count += (num == candidate) ? 1 : -1;
    }

    return candidate;
}

数组中只出现一次的数字

问题

【LeetCode 136】：你一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。

$O(n)$ 思路

• 使用集合存储数字。遍历数组中的每个数字，如果集合中没有该数字，则将该数字加入集合，如果集合中已经有该数字，则将该数字从集合中删除，最后剩下的数字就是只出现一次的数字。

• 使用哈希表存储每个数字和该数字出现的次数。遍历数组即可得到每个数字出现的次数，并更新哈希表，最后遍历哈希表，得到只出现一次的数字。

• 使用集合存储数组中出现的所有数字，并计算数组中的元素之和。由于集合保证元素无重复，因此计算集合中的所有元素之和的两倍，即为每个元素出现两次的情况下的元素之和。由于数组中只有一个元素出现一次，其余元素都出现两次，因此用集合中的元素之和的两倍减去数组中的元素之和，剩下的数就是数组中只出现一次的数字。

最优解：位运算

异或运算 $⊕$：

1. 任何数和 0 做异或运算，结果仍然是原来的数，即 $a⊕0=a$
2. 任何数和其自身做异或运算，结果是 000，即 $a⊕a=0$，即相同为 1，不同为 0
3. 异或运算满足交换律和结合律

假设数组中有 $2m+1$ 个数，其中有 $m$ 个数各出现两次，一个数出现一次。令 $a1、a_2、\ldots…、a_m$ 为出现两次的 $m$ 个数，$a{m+1}$ 为出现一次的数。根据性质 3，数组中的全部元素的异或运算结果总是可以写成如下形式：

$$(a_1​⊕a_1)⊕(a_2⊕a_2)⊕⋯⊕(a_m⊕a_m)⊕a_{m+1}$$

根据性质 2 和性质 1，上式可化简和计算得到如下结果：

$$0⊕0⊕⋯⊕0⊕a_{m+1}=a_{m+1}$$

因此，数组中的全部元素的异或运算结果即为数组中只出现一次的数字。

public int singleNumber(int[] nums) {
    int single = 0;
    for (int num : nums) {
        single ^= num;
    }
    return single;
}

一般解：Set 集合

当添加的元素在集合中已经存在时，不再进行添加操作，而是将集合中该元素删除，最终集合余下的元素便是只出现一次的数字

public int singleNumber(int[] nums) {

    Set<Integer> set = new HashSet<>();
    for (int num : nums) {
        // 当元素第一次出现，添加进集合，set.add(num) 返回 true
        // 当元素第二次出现时，此时集合中已经有了该元素，set.add(num) 返回 false
        if (!set.add(num)) { // if 当且仅当 true 才执行，因此取反
            // 将第二次出现的元素干掉
            set.remove(num);
            
        }
    }
    // 处理边界
    if (set.size() == 0) {
        return 0;
    }
    
    return set.toArray(new Integer[0])[0];
    
}

荷兰旗问题

问题

【LeetCode 75】：给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

必须在不使用库内置的 sort 函数的情况下解决这个问题。

单指针

可以考虑对数组进行两次遍历。在第一次遍历中，我们将数组中所有的 0 交换到数组的头部。在第二次遍历中，我们将数组中所有的 1 交换到头部的 0 之后。此时，所有的 2 都出现在数组的尾部，这样我们就完成了排序。

使用一个指针 ptr 表示「头部」的范围， ptr 中存储了一个整数，表示数组 nums 从位置 0 到位置 ptr−1 都属于「头部」。 ptr 的初始值为 0，表示还没有数处于「头部」。

在第一次遍历中，我们从左向右遍历整个数组，如果找到了 0，那么就需要将 0 与「头部」位置的元素进行交换，并将「头部」向后扩充一个位置。在遍历结束之后，所有的 0 都被交换到「头部」的范围，并且「头部」只包含 0。

在第二次遍历中，我们从「头部」开始，从左向右遍历整个数组，如果找到了 1，那么就需要将 1 与「头部」位置的元素进行交换，并将「头部」向后扩充一个位置。在遍历结束之后，所有的 1 都被交换到「头部」的范围，并且都在 0 之后，此时 2 只出现在「头部」之外的位置，因此排序完成。

public void sortColors(int[] nums) {

    // 使用一个指针 `ptr` 表示「头部」的范围
    // `ptr` 值表示从位置 `0` 到位置 `ptr−1` 都属于「头部」
    int ptr = 0;

    // 在第一次遍历中，从左向右遍历整个数组，
    // 如果找到 `0`，那么就需要将 `0` 与「头部」位置的元素进行交换，
    // 并将「头部」向后扩充一个位置。
    // 遍历结束后，所有的 `0` 都被交换到「头部」的范围，并且「头部」只包含 `0`。
    for (int i = 0; i < nums.length; i++) {
        if (nums[i] == 0) {
            int temp = nums[i];
            nums[i] = nums[ptr];
            nums[ptr] = temp;
            ++ptr;
        }
    }

    // 在第二次遍历中，从「头部」开始，从左向右遍历整个数组
    // 如果找到 `1`，那么就需要将 `1` 与「头部」位置的元素进行交换，
    // 并将「头部」向后扩充一个位置。
    // 在遍历结束之后，所有的 `1` 都被交换到「头部」的范围，并且都在 `0` 之后
    // 此时 `2` 只出现在「头部」之外的位置，因此排序完成。
    for (int i = ptr; i < nums.length; ++i) {
        if (nums[i] == 1) {
            int temp = nums[i];
            nums[i] = nums[ptr];
            nums[ptr] = temp;
            ++ptr;
        }
    }

}

双指针

• left 表示其左侧元素都是 0
  = right 表示其右侧元素都是 1
• index 表示当前处理的数字。从头到尾遍历数组，根据 nums[index] 是 0 还是 2 决定与left 交换还是与 right 交换

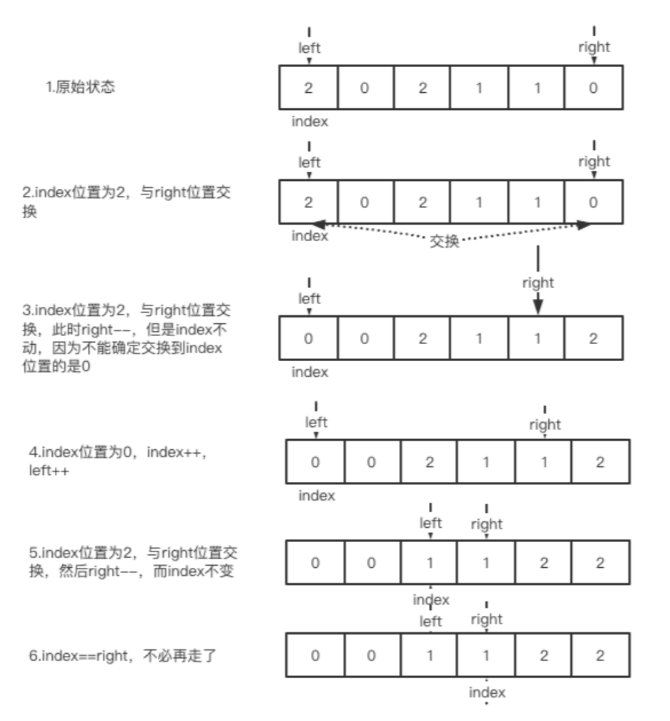
1. 当 index 为 0，将其放置左区间；
2. 当 index 为 1，不进行任何操作，直接 index++；
3. 当 index 为 2，将其放置右区间
4. 若 index==right，则停止操作

public void sortColors(int[] nums) {

    int index = 0;
    int left = 0, right = nums.length - 1;

    while (index <= right) {
        if (nums[index] == 0) {
            swap(nums, index++, left++);
        } else if (nums[index] == 2) {
            swap(nums, index, right--);
        } else
            index++;
    }

}

public void swap(int[] nums, int left, int right) {

    int temp = nums[left];
    nums[left] = nums[right];
    nums[right] = temp;
}

重点补充：

• nums[index] == 0：当前元素是红色时，将其交换到红色部分的末尾（left 指针所在位置），然后将 left 向后移动。这是因为红色部分已经包含了所有红色元素，我们知道当前元素是红色后，将其交换到红色部分的末尾是正确的，所以我们可以安全地将 index 指针向前移动。
• nums[index] == 2：当前元素是蓝色时，不能确定交换后的元素是什么颜色，因此不能直接将 index 指针向前移动。我们只是将当前元素交换到蓝色部分，但不确定新的元素是红色、白色还是蓝色。因此，在处理蓝色元素后，我们不移动 index 指针，因为我们将下次循环中去判断 index的颜色