栈专题—栈基础
通关进度
参考资料
一网打尽队栈结构
数组栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| public class AStack<T> {
private T[] stack;
private int top;
public AStack() {
this.stack = (T[]) new Object[10];
}
public boolean isEmpty() {
return top == 0;
}
public T peek() {
T t = null;
if (top > 0) {
t = stack[top - 1];
}
return t;
}
public T pop() {
T t = peek();
if (top > 0) {
stack[top - 1] = null;
top--;
}
return t;
}
public void push(T t) {
expandCapacity(top + 1);
stack[top++] = t;
}
public void expandCapacity(int size) {
int length = stack.length;
if (size > length) {
size = size * 3 / 2 + 1;
stack = Arrays.copyOf(stack, size);
}
}
}
|
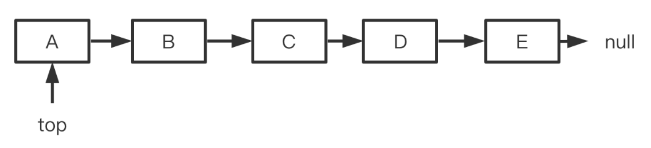
链表栈
链表实现栈:在头节点进行插入和删除节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| public class LStack<T> {
class Node<T> {
public T data;
public Node next;
}
public Node<T> head;
public LStack() {
this.head = null;
}
public void push(T t) {
if (t == null) {
throw new NullPointerException("参数不能为空");
}
if (head == null) {
head = new Node<>();
head.data = t;
head.next = null;
} else {
Node<T> temp = head;
head = new Node<>();
head.data = t;
head.next = temp;
}
}
public T pop() {
if (head == null) {
return null;
}
T t = head.data;
head = head.next;
return t;
}
public T peek() {
if (head == null) {
return null;
}
return head.data;
}
public boolean isEmpty() {
return head == null;
}
}
|
栈专题—栈强化
通关进度
| 题目 |
说明 |
| 括号匹配问题 |
通关 |
| 最小栈 |
通关 |
| 最大栈 |
通关 |
括号匹配问题
20. 有效的括号
问题
【LettCode 20】:给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号。
算法思路
- 当遇到一个左括号时,会期望在后续的遍历中,有一个相同类型的右括号将其闭合。由于后遇到的左括号要先闭合,因此可以将这个左括号放入栈顶。
- 当遇到一个右括号时,需要将一个相同类型的左括号闭合。此时,可以取出栈顶的左括号并判断它们是否是相同类型的括号。如果不是相同的类型,或者栈中并没有左括号,那么字符串 s 无效,返回 False。
为快速判断括号的类型,可以使用哈希表存储每一种括号。哈希表的键为右括号,值为相同类型的左括号。
在遍历结束后,如果栈中没有左括号,说明将字符串 s 中的所有左括号闭合,返回 True,否则返回 False。
注意到有效字符串的长度一定为偶数,因此如果字符串的长度为奇数,我们可以直接返回 False,省去后续的遍历判断过程。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| public boolean isValid(String s) {
if (s.length() % 2 == 1) {
return false;
}
Map<Character, Character> pairs = new HashMap<>();
pairs.put(')', '(');
pairs.put('}', '{');
pairs.put(']', '[');
Stack<Character> stack = new Stack<>();
for (int i = 0; i < s.length(); i++) {
char ch = s.charAt(i);
if (pairs.containsKey(ch)) {
if (stack.isEmpty() || stack.peek() != pairs.get(ch)) {
return false;
}
stack.pop();
} else {
stack.push(ch);
}
}
return stack.isEmpty();
}
|
扩展
LeetCode 22.括号生成
LeetCode 32.最长有效括号
LeetCode 301.删除无效的括号
LeetCode 856.括号的分数
最小栈
155. 最小栈
问题
【LeetCode 155】:设计一个支持 push,pop,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack() 初始化堆栈对象。void push(int val) 将元素val推入堆栈。void pop() 删除堆栈顶部的元素。int top() 获取堆栈顶部的元素。int getMin() 获取堆栈中的最小元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| 输入:
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]
输出:
[null,null,null,null,-3,null,0,-2]
解释:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.
|
注意
题目要求在常数时间内获得栈最小值,因此不能在 getMin() 时再计算最小值
栈的性质
对于栈来说,如果一个元素 a 在入栈时,栈里有其它的元素 b, c, d,那么无论这个栈在之后经历了什么操作,只要 a 在栈中,b, c, d 就一定在栈中,因为在 a 被弹出之前,b, c, d 不会被弹出。
因此,在操作过程中的任意一个时刻,只要栈顶的元素是 a,那么我们就可以确定栈里面现在的元素一定是 a, b, c, d。
那么,我们可以在每个元素 a 入栈时把当前栈的最小值 m 存储起来。在这之后无论何时,如果栈顶元素是 a,我们就可以直接返回存储的最小值 m。
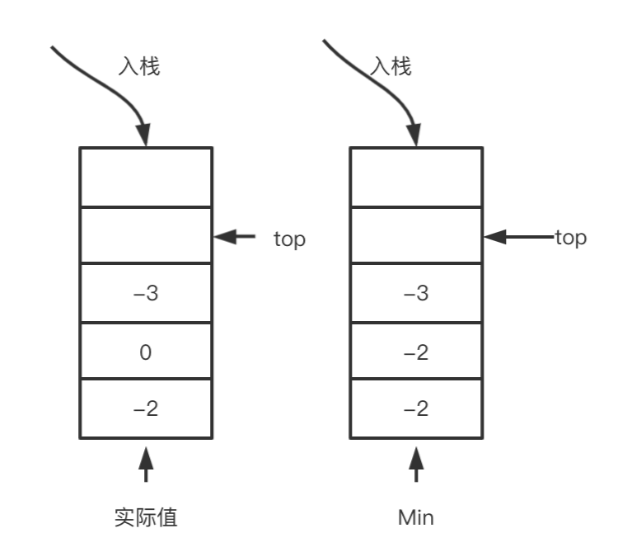
只需要设计一个数据结构,使得每个元素 a 与其相应的最小值 m 时刻保持一一对应,可以使用一个辅助栈,与元素栈同步插入与删除,用于存储与每个元素对应的最小值。
当一个元素要入栈时,取当前辅助栈的栈顶存储的最小值,与当前元素比较得出最小值,将这个最小值插入辅助栈中;
当一个元素要出栈时,把辅助栈的栈顶元素也一并弹出;
在任意一个时刻,栈内元素的最小值就存储在辅助栈的栈顶元素中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| public class MinStack {
private Deque<Integer> stack;
private Deque<Integer> minStack;
public MinStack() {
stack = new LinkedList<>();
minStack = new LinkedList<>();
minStack.push(Integer.MAX_VALUE);
}
public void push(int x) {
stack.push(x);
minStack.push(Math.min(x, minStack.peek()));
}
public void pop() {
stack.pop();
minStack.pop();
}
public int top() {
return stack.peek();
}
public int getMin() {
return minStack.peek();
}
}
|
最大栈
问题
【LeetCode 716】:设计一个支持 push,pop,top 操作,并能在常数时间内检索到最大元素的栈。
实现 MaxStack 类:
MaxStack() 初始化栈对象push(x) 将元素 x 压入栈中pop() 移除栈顶元素并返回这个值top() 返回栈顶元素peekMax() 返回栈中最大元素popMax() 返回栈中最大的元素,并将其删除 如果有多个最大元素,只要删除最靠近栈顶的那个。
1
2
3
4
5
6
7
8
9
10
| MaxStack stack = new MaxStack();
stack.push(5);
stack.push(1);
stack.push(5);
stack.top(); -> 5
stack.popMax(); -> 5
stack.top(); -> 1
stack.peekMax(); -> 5
stack.pop(); -> 1
stack.top(); -> 5
|
peekMax
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| public class MaxStack {
private Deque<Integer> stack;
private Deque<Integer> maxStack;
public MaxStack() {
this.stack = new LinkedList<>();
this.maxStack = new LinkedList<>();
}
public void push(int x) {
int max = maxStack.isEmpty() ? x : maxStack.peek();
maxStack.push(max > x ? max : x);
stack.push(x);
}
public int pop() {
maxStack.pop();
return stack.pop();
}
public int top() {
return stack.peek();
}
public int peekMax() {
return maxStack.peek();
}
public int popMax() {
int max = peekMax();
Deque<Integer> temp = new LinkedList<>();
while (top() != max) {
temp.push(pop());
}
pop();
while (!temp.isEmpty()) {
push(temp.pop());
}
return max;
}
}
|
栈专题—表达式栈
通关进度
计算器问题
227. 基本计算器 II
问题
【LeetCode 227】:给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
整数除法仅保留整数部分。
你可以假设给定的表达式总是有效的。所有中间结果将在 $[-2^{31}, 2^{31} - 1]$ 的范围内。
栈
由于乘除优先于加减计算,因此不妨考虑先进行所有乘除运算,并将这些乘除运算后的整数值放回原表达式的相应位置,则随后整个表达式的值,就等于一系列整数加减后的值。
基于此,可以用一个栈,保存进行乘除运算后的值。对于加减号后的数字,将其直接压入栈中;对于乘除号后的数字,可以直接与栈顶元素计算,并替换栈顶元素为计算后的结果。
具体来说,遍历字符串 s,并用变量 preSign 记录每个数字之前的运算符,对于第一个数字,其之前的运算符视为加号。每次遍历到数字末尾时,根据 preSign 来决定计算方式:
- 加号:将数字压入栈;
- 减号:将数字的相反数压入栈;
- 乘除号:计算数字与栈顶元素,并将栈顶元素替换为计算结果。
代码实现中,若读到一个运算符,或者遍历到字符串末尾,即认为是遍历到了数字末尾。处理完该数字后,更新 preSign 为当前遍历的字符。
遍历完字符串 s 后,将栈中元素累加,即为该字符串表达式的值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| public int calculate(String s) {
Deque<Integer> stack = new ArrayDeque<Integer>();
char preSign = '+';
int num = 0;
int n = s.length();
for (int i = 0; i < n; ++i) {
if (Character.isDigit(s.charAt(i))) {
num = num * 10 + s.charAt(i) - '0';
}
if (!Character.isDigit(s.charAt(i)) && s.charAt(i) != ' ' || i == n - 1) {
switch (preSign) {
case '+':
stack.push(num);
break;
case '-':
stack.push(-num);
break;
case '*':
stack.push(stack.pop() * num);
break;
default:
stack.push(stack.pop() / num);
}
preSign = s.charAt(i);
num = 0;
}
}
int ans = 0;
while (!stack.isEmpty()) {
ans += stack.pop();
}
return ans;
}
|
逆波兰表达式
150. 逆波兰表达式求值
问题
【LeetCode 150】:给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
注意:
- 有效的算符为
'+'、'-'、'*' 和 '/' 。
- 每个操作数(运算对象)都可以是一个整数或者另一个表达式。
- 两个整数之间的除法总是 向零截断 。
- 表达式中不含除零运算。
- 输入是一个根据逆波兰表示法表示的算术表达式。
- 答案及所有中间计算结果可以用 32 位 整数表示。
栈
逆波兰表达式严格遵循「从左到右」的运算。计算逆波兰表达式的值时,使用一个栈存储操作数,从左到右遍历逆波兰表达式,进行如下操作:
整个逆波兰表达式遍历完毕之后,栈内只有一个元素,该元素即为逆波兰表达式的值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| public int evalRPN(String[] tokens) {
Deque<Integer> stack = new LinkedList<Integer>();
int n = tokens.length;
for (int i = 0; i < n; i++) {
String token = tokens[i];
if (isNumber(token)) {
stack.push(Integer.parseInt(token));
} else {
int num2 = stack.pop();
int num1 = stack.pop();
switch (token) {
case "+":
stack.push(num1 + num2);
break;
case "-":
stack.push(num1 - num2);
break;
case "*":
stack.push(num1 * num2);
break;
case "/":
stack.push(num1 / num2);
break;
default:
}
}
}
return stack.pop();
}
public boolean isNumber(String token) {
return !("+".equals(token) || "-".equals(token) || "*".equals(token) || "/".equals(token));
}
|
说明
前缀表达式的运算符位于操作数之前,中缀和后缀同理,其实本质对应二叉树前/中/后序遍历方式











