二叉树专题Ⅰ—树结构

通关进度

题目	说明
使用前中序列构造二叉树	通关
使用中后序列构造二叉树	通关

树的常见概念

树是一个有 $n$ 个有限节点组成一个具有层次关系的集合，每个节点有 $0$ 个或者多个子节点，没有父节点的节点称为根节点

节点的度：一个节点含有的子节点的个数称为该节点的度
树的度：一棵树中，最大的节点的度称为树的度，注意与节点度的区别
叶节点或终端节点：度为 $0$ 的节点称为叶节点
非终端节点或分支节点：度不为 $0$ 的节点
双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点
孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点
兄弟节点：具有相同父节点的节点互称为兄弟节点
节点的祖先：从根到该节点所经分支上的所有节点
子孙：以某节点为根的子树中任一节点都称为该节点的子孙
森林：由 $m(m>=0)$ 棵互不相交的树的集合称为森林
无序树：树中任意节点的子节点之间没有顺序关系，也称为自由树:
有序树：树中任意节点的子节点之间有顺序关系
二叉树：每人节点最多含有两人子树的树称为二叉树

树的性质

性质 1：在二又树的第 $i$ 层上至多有 $2^{i-1}$ 个结点 ($i>0$)
性质 2：深度为 $k$ 的二又树至多有 $2^k - 1$ 个结点 ($k>0$)
性质 3：对于任意一棵二又树，如果其叶结点数为 $N_O$，而度数为 2 的结点总数为 $N_2$，则 $N_O=N_2+1$
性质 4：具有n个结点的完全二叉树的深度必为 $log2(n+1)$
性质 5：对完全二叉树，若从上至下、从左至右编号，则编号为 $i$ 的结点，其左孩子编号必为 $2i$
其右孩了编号必为 $2i+ 1$；其双亲的编号必为 $i/2$ ($i= 1$ 时为根，除外)

完全二叉树（Complete Binary Tree）：

满二叉树和完全二又树是经常晕的问题，我们有必要单独看一下。满二叉树就是如果一棵二又树只有度为 0 的节点和度为2的节点，并目度为 0 的节点在同一层上，则这棵二叉树为满二叉树。

满二叉树（Full Binary Tree）：

在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。

树的定义与存储方式

2-Tree

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
}

N-Tree

public class TreeNode {
    int val;
    List<TreeNode> nodes;
}

树的遍历方式

前序遍历
中序遍历
后序遍历

通过序列构造二叉树

使用前中序列构造二叉树

105. 从前序与中序遍历序列构造二叉树

问题

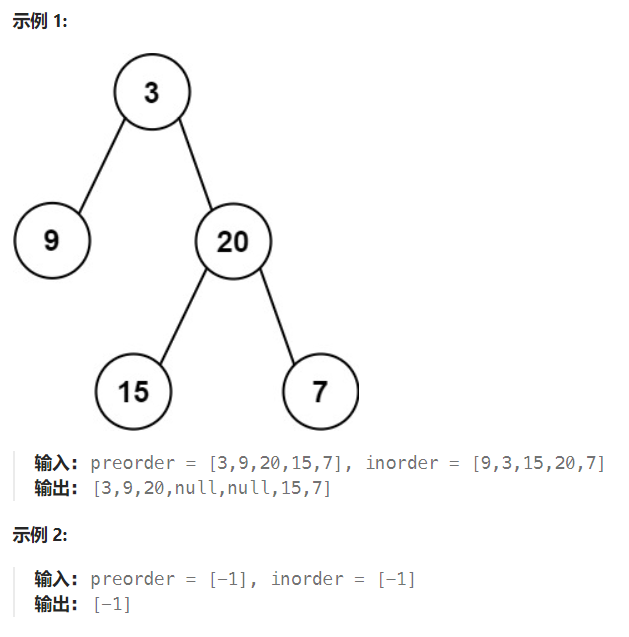
【LeetCode 105】：给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

递归

对于任意一颗树而言，前序遍历的形式总是

1	[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]

即根节点总是前序遍历中的第一个节点。而中序遍历的形式总是

1	[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]

只要我们在中序遍历中定位到根节点，那么我们就可以分别知道左子树和右子树中的节点数目。由于同一颗子树的前序遍历和中序遍历的长度显然是相同的，因此我们就可以对应到前序遍历的结果中，对上述形式中的所有左右括号进行定位。
这样一来，我们就知道了左子树的前序遍历和中序遍历结果，以及右子树的前序遍历和中序遍历结果，我们就可以递归地对构造出左子树和右子树，再将这两颗子树接到根节点的左右位置。

细节

在中序遍历中对根节点进行定位时，一种简单的方法是直接扫描整个中序遍历的结果并找出根节点，但这样做的时间复杂度较高。
可以考虑使用哈希表快速定位根节点。对于哈希映射中的每个键值对，键表示一个元素（节点的值），值表示其在中序遍历中的出现位置。在构造二叉树的过程之前，可以对中序遍历的列表进行一遍扫描，就可以构造出这个哈希映射。在此后构造二叉树的过程中，只需要 $O(1)$ 的时间对根节点进行定位。

private Map<Integer, Integer> indexMap;

public TreeNode myBuildTree(int[] preorder, int[] inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
    if (preorder_left > preorder_right) {
        return null;
    }

    // 前序遍历中的第一个节点就是根节点
    int preorder_root = preorder_left;
    // 在中序遍历中定位根节点
    int inorder_root = indexMap.get(preorder[preorder_root]);

    // 先把根节点建立出来
    TreeNode root = new TreeNode(preorder[preorder_root]);
    // 得到左子树中的节点数目
    int size_left_subtree = inorder_root - inorder_left;
    // 递归地构造左子树，并连接到根节点
    // 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
    root.left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
    // 递归地构造右子树，并连接到根节点
    // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
    root.right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
    return root;
    
}
public TreeNode buildTree(int[] preorder, int[] inorder) {
    int n = preorder.length;
    // 构造哈希映射，帮助我们快速定位根节点
    indexMap = new HashMap<>();
    for (int i = 0; i < n; i++) {
        indexMap.put(inorder[i], i);
    }
    return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
}

使用中后序列构造二叉树

106. 从中序与后序遍历序列构造二叉树

问题

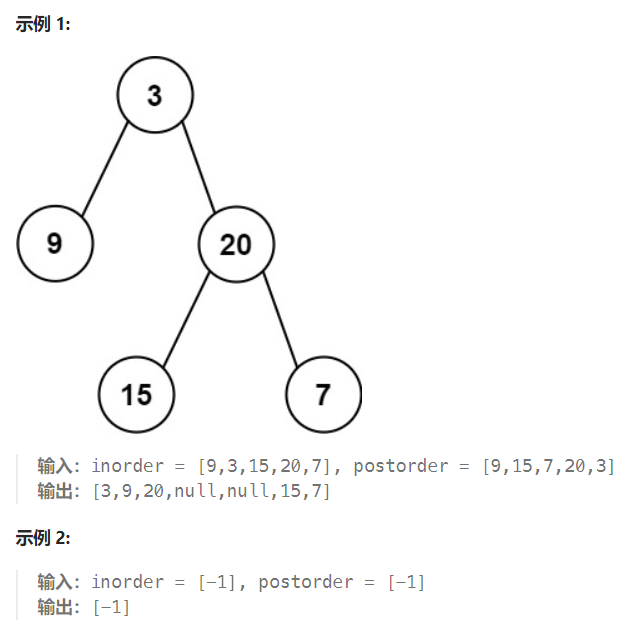
【LeetCode 106】：给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗二叉树。

递归

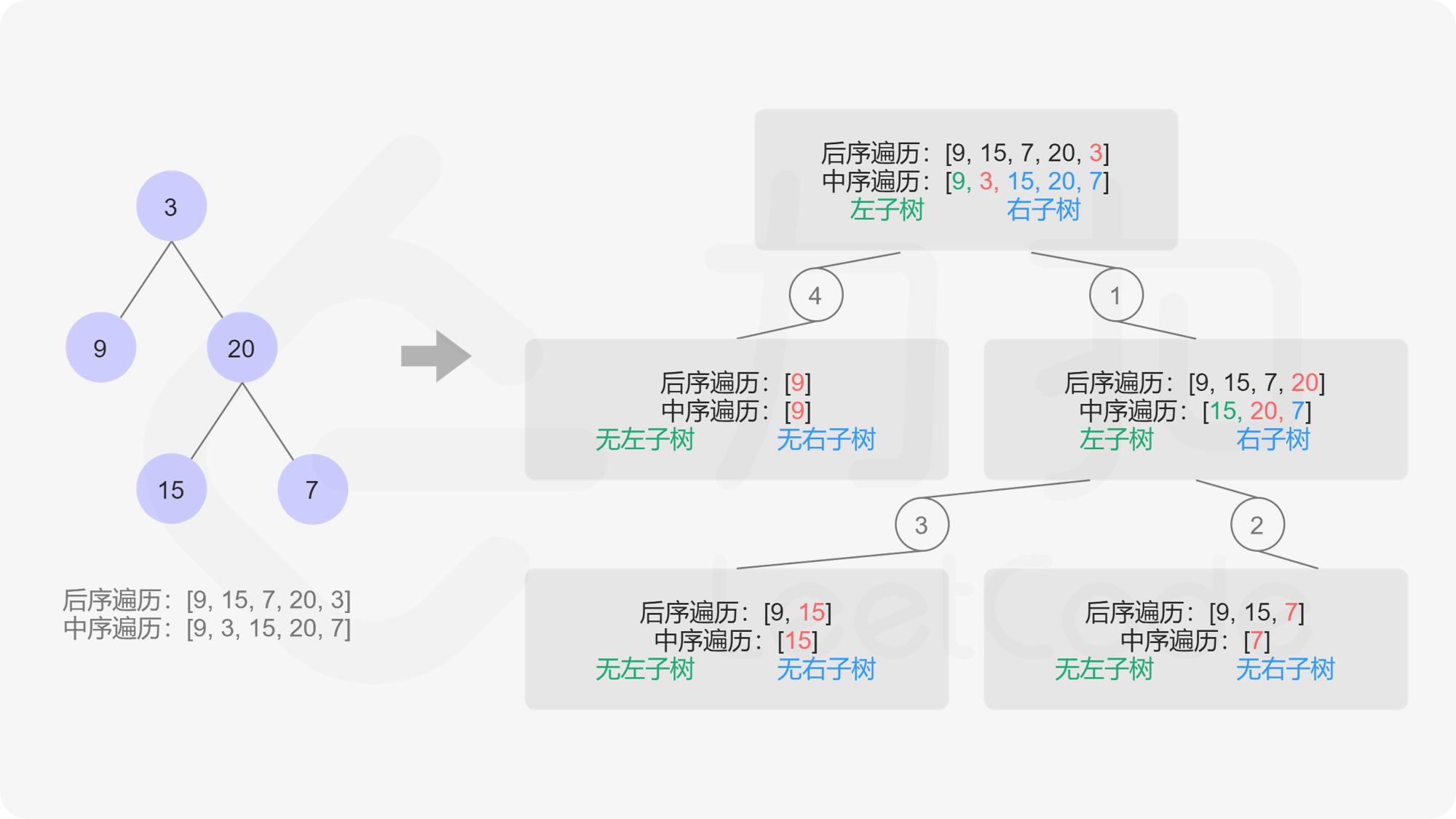
为高效查找根节点元素在中序遍历数组中的下标，选择创建哈希表来存储中序序列，即建立一个（元素，下标）键值对的哈希表
定义递归函数 helper(in_left, in_right) 表示当前递归到中序序列中当前子树的左右边界，递归入口为 helper(0, n - 1) ：

如果 in_left > in_right，说明子树为空，返回空节点
选择后序遍历的最后一个节点作为根节点
利用哈希表 $O(1)$ 查询当根节点在中序遍历中下标为 index。从 in_left 到 index - 1 属于左子树，从 index + 1 到 in_right 属于右子树。
- 根据后序遍历逻辑，递归创建右子树 helper(index + 1, in_right) 和左子树 helper(in_left, index - 1)
- 返回根节点 root
  注意这里有需要先创建右子树，再创建左子树的依赖关系。可以理解为在后序遍历的数组中整个数组是先存储左子树的节点，再存储右子树的节点，最后存储根节点，如果按每次选择「后序遍历的最后一个节点」为根节点，则先被构造出来的应该为右子树。

private int post_idx;
private int[] postorder;
private int[] inorder;
private Map<Integer, Integer> idx_map = new HashMap<Integer, Integer>();

public TreeNode helper(int in_left, int in_right) {
    // 如果这里没有节点构造二叉树了，就结束
    if (in_left > in_right) {
        return null;
    }

    // 选择 post_idx 位置的元素作为当前子树根节点
    int root_val = postorder[post_idx];
    TreeNode root = new TreeNode(root_val);

    // 根据 root 所在位置分成左右两棵子树
    int index = idx_map.get(root_val);

    // 下标减一
    post_idx--;
    // 构造右子树
    root.right = helper(index + 1, in_right);
    // 构造左子树
    root.left = helper(in_left, index - 1);
    return root;
}

public TreeNode buildTree(int[] inorder, int[] postorder) {
    this.postorder = postorder;
    this.inorder = inorder;
    // 从后序遍历的最后一个元素开始
    post_idx = postorder.length - 1;

    // 建立（元素，下标）键值对的哈希表
    int idx = 0;
    for (Integer val : inorder) {
        idx_map.put(val, idx++);
    }

    return helper(0, inorder.length - 1);
}

二叉树专题Ⅰ—二叉树的层次遍历

通关进度

题目	说明
二叉树的层次遍历	通关
使用中后序列构造二叉树	通关
自底向上的层次遍历	通关
二叉树的锯齿形层序遍历	通关
N 叉树层次遍历	通关
在每个树行中找最大值	通关
二叉树的层平均值	通关
二叉树右视图	通关
二叉树的最底层最左边	通关
左叶子之和	通关

层次遍历

二叉树的层次遍历

102. 二叉树的层序遍历

问题

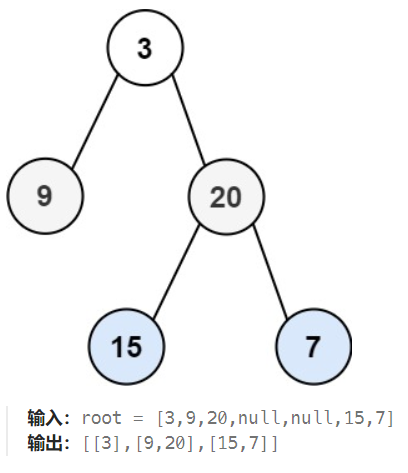
【LeetCode 102】：给你二叉树的根节点 root ，返回其节点值的层序遍历。（即逐层地，从左到右访问所有节点）。

广度优先搜索

使用一种巧妙的方法修改广度优先搜索：

首先根元素入队
当队列不为空时
- 求当前队列长度 $s_i$
- 依次从队列中取 $s_i$ 个元素进行拓展，然后进入下一次迭代

public List<List<Integer>> levelOrder(TreeNode root) {

    // 存储结果
    List<List<Integer>> ret = new ArrayList<>();
    // base case
    if (root == null) {
        return ret;
    }
    // 队列
    Queue<TreeNode> queue = new LinkedList<>();
    // 根元素入队
    queue.offer(root);

    // 当队列不为空时
    while (!queue.isEmpty()) {
        // 当前层次
        List<Integer> level = new ArrayList<>();
        // 当前队列长度（当前层元素个数）
        int currentLevelSize = queue.size();
        // 依次取 currentLevelSize 元素拓展
        for (int i = 0; i < currentLevelSize; i++) {
            // 出队该元素
            TreeNode node = queue.poll();
            // 将 node 元素放入 level
            level.add(node.val);
            // 入队左孩子
            if (node.left != null) {
                queue.offer(node.left);
            }
            // 入队右孩子
            if (node.right != null) {
                queue.offer(node.left);
            }
        }
        // 将当前层次放入结果中，准备下一次迭代
        ret.add(level);
    }
    return ret;
}

自底向上的层次遍历

107. 二叉树的层序遍历 II

问题

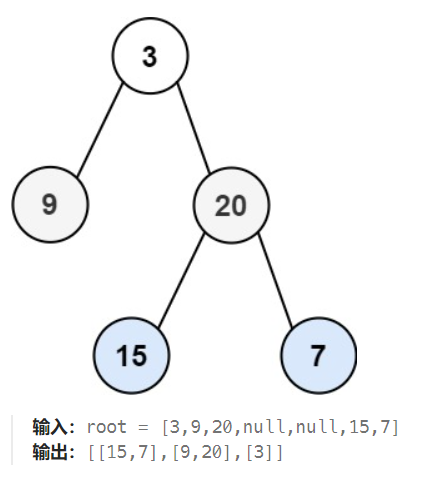
【LeetCode 107】：给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。（即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

广度优先搜索

从根节点开始搜索，每次遍历同一层的全部节点，使用一个列表存储该层的节点值
如果要求从上到下输出每一层的节点值，在遍历完一层节点之后，将存储该层节点值的列表添加到结果列表的尾部
这道题要求从下到上输出每一层的节点值，只要对上述操作稍作修改即可：在遍历完一层节点之后，将存储该层节点值的列表添加到结果列表的头部

public List<List<Integer>> levelOrderBottom(TreeNode root) {

    // 存储结果
    List<List<Integer>> levelOrder = new LinkedList<>();
    // base case
    if (root == null) {
        return levelOrder;
    }
    // 队列
    Queue<TreeNode> queue = new LinkedList<>();
    // 入队根元素
    queue.offer(root);
    // 当队列不为空时
    while (!queue.isEmpty()) {
        // 当前层次
        List<Integer> level = new ArrayList<>();
        // 当前队列长度（当前层元素个数）
        int currentLevelSize = queue.size();
        // 依次取 currentLevelSize 元素拓展
        for (int i = 0; i < currentLevelSize; i++) {
            TreeNode node = queue.poll();
            level.add(node.val);
            TreeNode left = node.left, right = node.right;
            if (left != null) {
                queue.offer(left);
            }
            if (right != null) {
                queue.offer(right);
            }
        }
        // 在遍历完一层节点之后，将存储该层节点值的列表添加到结果列表的头部 
        levelOrder.add(0, level);
    }
    return levelOrder;
}

二叉树的锯齿形层序遍历

103. 二叉树的锯齿形层序遍历

题目

【LeetCode 103】：给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

广度优先搜索

规定二叉树的根节点为第 0 层，如果当前层数是偶数，从左至右输出当前层的节点值，否则，从右至左输出当前层的节点值
对树进行逐层遍历，用队列维护当前层的所有元素，当队列不为空时，求得当前队列的长度 size，每次从队列中取出 size 个元素进行拓展，然后进行下一次迭代。
为满足题目要求的返回值为「先从左往右，再从右往左」交替输出的锯齿形，可以利用「双端队列」的数据结构来维护当前层节点值输出的顺序

双端队列是一个可以在队列任意一端插入元素的队列。在广度优先搜索遍历当前层节点拓展下一层节点的时候我们仍然从左往右按顺序拓展，但是对当前层节点的存储我们维护一个变量 isOrderLeft 记录是从左至右还是从右至左的：

如果从左至右，我们每次将被遍历到的元素插入至双端队列的末尾
如果从右至左，我们每次将被遍历到的元素插入至双端队列的头部

public List<List<Integer>> zigzagLevelOrder(TreeNode root) {

    // 结果
    List<List<Integer>> ans = new LinkedList<>();
    // base case
    if (root == null) {
        return ans;
    }
    // 队列
    Queue<TreeNode> queue = new ArrayDeque<>();
    // 入队根元素
    queue.offer(root);
    // 奇偶标记
    boolean isOrderLeft = true;

    while (!queue.isEmpty()) {
        // 当前层次
        Deque<Integer> levelList = new LinkedList<>();
        // 当前队列长度（当前层元素个数）
        int currentLevelSize = queue.size();
        for (int i = 0; i < currentLevelSize; i++) {
            TreeNode curNode = queue.poll();
            if (isOrderLeft) {
                levelList.offerLast(curNode.val);
            } else {
                levelList.offerFirst(curNode.val);
            }
            if (curNode.left != null) {
                queue.offer(curNode.left);
            }
            if (curNode.right != null) {
                queue.offer(curNode.right);
            }
        }
        // 将当前层次元素装入 ans
        ans.add(new LinkedList<>(levelList));
        // 奇偶反转
        isOrderLeft = !isOrderLeft;
    }
    return ans;
}

N 叉树层次遍历

429. N 叉树的层序遍历

问题

【LeetCode 429】：给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

广度优先搜索

对于「层序遍历」的题目，一般使用广度优先搜索。在广度优先搜索的每一轮中，会遍历同一层的所有节点
首先把根节点 root 放入队列中，随后在广度优先搜索的每一轮中，首先记录下当前队列中包含的节点个数（记为 cnt），即表示上一层的节点个数
在这之后，从队列中依次取出节点，直到取出上一层的全部 cnt 个节点为止
当取出节点 cur 时，将 cur 的值放入一个临时列表，再将 cur 的所有子节点全部放入队列中

当这一轮遍历完成后，临时列表则存放着当前层所有节点的值。当整个广度优先搜索完成后，就可以得到层序遍历的结果。

public List<List<Integer>> levelOrder(Node root) {
    // base case
    if (root == null) {
        return new ArrayList<>();
    }

    List<List<Integer>> ans = new ArrayList<>();
    // 队列
    Queue<Node> queue = new ArrayDeque<>();
    // 入队根元素
    queue.offer(root);

    // 当队列不为空时
    while (!queue.isEmpty()) {
        // 当前队列中包含的节点个数 cnt
        int cnt = queue.size();
        // 临时列表
        List<Integer> level = new ArrayList<>();
        for (int i = 0; i < cnt; ++i) {
            // 出队 cur
            Node cur = queue.poll();
            // 将 cur 放入临时列表
            level.add(cur.val);
            for (Node child : cur.children) {
                queue.offer(child);
            }
        }
        ans.add(level);
    }

    return ans;
}

在每个树行中找最大值

515. 在每个树行中找最大值

问题

【LeetCode 515】：给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

广度优先搜索

「广度优先搜索」中的队列里存放的是「当前层的所有节点」
把当前队列中的全部节点拿出来进行拓展，这样能保证每次拓展完的时候队列里存放的是下一层的所有节点
即一层一层地进行拓展，然后每一层用 maxVal 来标记该层节点的最大值
当该层全部节点都处理完后，maxVal 就是该层全部节点中的最大值

public List<Integer> largestValues(TreeNode root) {

    if (root == null) {
        return new ArrayList<>();
    }
    // 结果集
    List<Integer> res = new ArrayList<>();
    // 队列
    Queue<TreeNode> queue = new ArrayDeque<>();
    // 根节点入队
    queue.offer(root);

    // 当队列不为空时
    while (!queue.isEmpty()) {
        // 当前层元素个数
        int cnt = queue.size();
        // max val
        int levelMaxVal = Integer.MIN_VALUE;

        for (int i = 0; i < cnt; ++i) {
            TreeNode node = queue.poll();
            levelMaxVal = Math.max(levelMaxVal, node.val);
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
        res.add(levelMaxVal);
    }
    return res;
}

二叉树的层平均值

637. 二叉树的层平均值

问题

【LeetCode 637】：给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 $10^{-5}$ 以内的答案可以被接受。

广度优先搜索

使用广度优先搜索计算二叉树的层平均值。从根节点开始搜索，每一轮遍历同一层的全部节点，计算该层的节点数以及该层的节点值之和，然后计算该层的平均值。

初始时，将根节点加入队列；
每一轮遍历时，将队列中的节点全部取出，计算这些节点的数量以及它们的节点值之和，并计算这些节点的平均值，然后将这些节点的全部非空子节点加入队列，重复上述操作直到队列为空，遍历结束。

public List<Double> averageOfLevels(TreeNode root) {
    // 平均值
    List<Double> averages = new ArrayList<>();
    // 队列
    Queue<TreeNode> queue = new LinkedList<>();
    // 入队根元素
    queue.offer(root);

    // 当队列不为空时
    while (!queue.isEmpty()) {
        // sum
        double sum = 0;
        // 当前层次元素数
        int size = queue.size();
        for (int i = 0; i < size; i++) {
            TreeNode node = queue.poll();
            sum += node.val;
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
        averages.add(sum / size);
    }
    return averages;
}

二叉树的右视图

199. 二叉树的右视图

问题

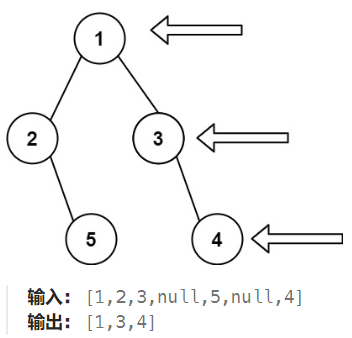
【LeetCode 199】：给定一个二叉树的根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

广度优先搜索

执行广度优先搜索，左结点排在右结点之前，对每一层都从左到右访问
只保留每个深度最后访问的结点，就可以在遍历完整棵树后得到每个深度最右的结点

public List<Integer> rightSideView(TreeNode root) {

    List<Integer> res = new ArrayList<>();
    // base case
    if (root == null) {
        return res;
    }
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);

    while (!queue.isEmpty()) {
        int cnt = queue.size();
        for (int i = 0; i < cnt; i++) {
            TreeNode node = queue.poll();
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
            if (i == cnt - 1) {
                // 将当前层最后一个节点放入列表
                res.add(node.val);
            }
        }
    }
    return res;
}

深度优先搜索

private List<Integer> ans;

public List<Integer> rightSideView(TreeNode root) {
    ans = new ArrayList<>();
    dfs(root, 0);
    return ans;
}

private void dfs(TreeNode node, int depth) {
    if (node == null) return;
    if (ans.size() <= depth)
        ans.add(node.val);
    else
        ans.set(depth, node.val);
    dfs(node.left, depth + 1);
    dfs(node.right, depth + 1);
}

找树左下角的值

513. 找树左下角的值

问题

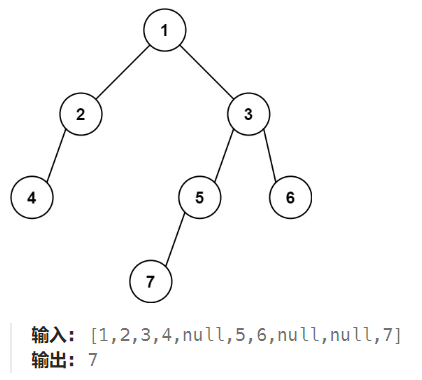
【LeetCode 513】：给定一个二叉树的根节点 root，请找出该二叉树的 最底层最左边 节点的值。
假设二叉树中至少有一个节点。

广度优先搜索

先反转，再入队列
使用广度优先搜索遍历每一层的节点。在遍历一个节点时，需要先把它的非空右子节点放入队列，然后再把它的非空左子节点放入队列，这样才能保证从右到左遍历每一层的节点。广度优先搜索所遍历的最后一个节点的值就是最底层最左边节点的值。

public int findBottomLeftValue(TreeNode root) {
    int ret = 0;
    Queue<TreeNode> queue = new ArrayDeque<>();
    queue.offer(root);
    while (!queue.isEmpty()) {
        TreeNode p = queue.poll();
        if (p.right != null) {
            queue.offer(p.right);
        }
        if (p.left != null) {
            queue.offer(p.left);
        }
        ret = p.val;
    }
    return ret;
}

左叶子之和

404. 左叶子之和

问题

【LeetCode 404】：给定二叉树的根节点 root ，返回所有左叶子之和。

一个节点为「左叶子」节点，当且仅当它是某个节点的左子节点，并且它是一个叶子结点。因此我们可以考虑对整棵树进行遍历，当我们遍历到节点 node 时，如果它的左子节点是一个叶子结点，那么就将它的左子节点的值累加计入答案。

DFS

public int sumOfLeftLeaves(TreeNode root) {
    return root != null ? dfs(root) : 0;
}

public int dfs(TreeNode node) {
    int ans = 0;
    if (node.left != null) {
        ans += isLeafNode(node.left) ? node.left.val : dfs(node.left);
    }
    if (node.right != null && !isLeafNode(node.right)) {
        ans += dfs(node.right);
    }
    return ans;
}

public boolean isLeafNode(TreeNode node) {
    return node.left == null && node.right == null;
}

BFS

public boolean isLeafNode(TreeNode node) {
    return node.left == null && node.right == null;
}

// BFS
public int sumOfLeftLeaves(TreeNode root) {
    if (root == null) {
        return 0;
    }
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    int ans = 0;

    while (!queue.isEmpty()) {
        TreeNode node = queue.poll();
        if (node.left != null) {
            if (isLeafNode(node.left)) {
                ans += node.left.val;
            } else {
                queue.offer(node.left);
            }
        }
        if (node.right != null) {
            if (!isLeafNode(node.right)) {
                queue.offer(node.right);
            }
        }
    }
    return ans;
}