二叉树 DFS 问题—经典问题
通关进度
| 题目 |
说明 |
| 判断两棵树是否相同 |
通关 |
| 判断两棵树是否对称 |
通关 |
| 合并两棵二叉树 |
通关 |
| 寻找二叉树所有路径 |
通关 |
| 路径总和问题 |
通关 |
| 翻转二叉树 |
通关 |
二叉树中的双指针
判断两棵树是否相同
100. 相同的树
问题
【LeetCode 100】:给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
DFS
- 如果两个二叉树都为空,则两个二叉树相同。如果两个二叉树中有且只有一个为空,则两个二叉树一定不相同。
- 如果两个二叉树都不为空,那么首先判断它们的根节点的值是否相同,若不相同则两个二叉树一定不同,若相同,再分别判断两个二叉树的左子树是否相同以及右子树是否相同。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| public boolean isSameTree(TreeNode p, TreeNode q) {
if (p == null && q == null) {
return true;
} else if (p == null || q == null) {
return true;
} else if (p.val != q.val){
return false;
} else {
return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
}
}
|
对称二叉树
101. 对称二叉树
问题
【LeetCode 101】:给你一个二叉树的根节点 root , 检查它是否轴对称。
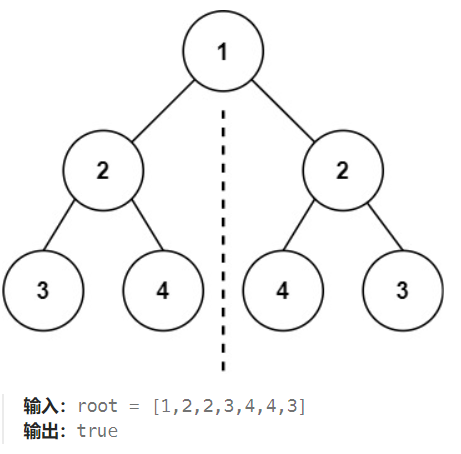
DFS
如果一个树的左子树与右子树镜像对称,那么这个树是对称的。
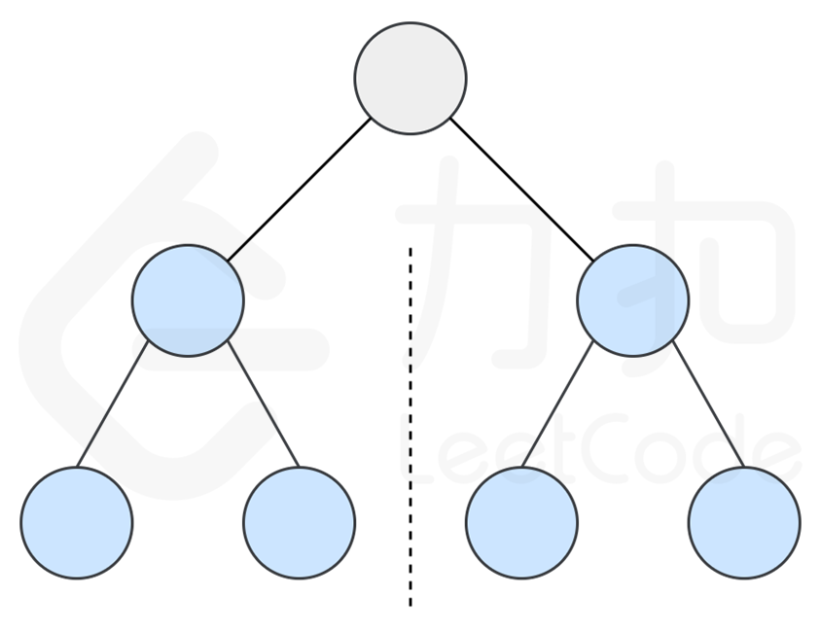
如果同时满足下面的条件,两个树互为镜像:
- 它们的两个根结点具有相同的值
- 每个树的右子树都与另一个树的左子树镜像对称
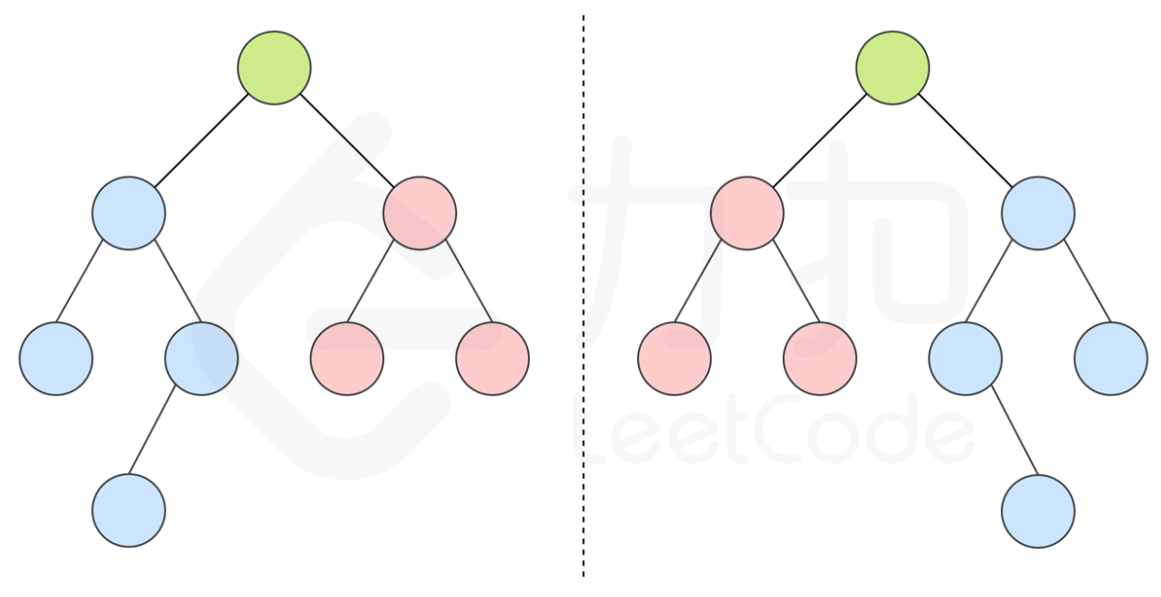
通过「同步移动」两个指针的方法来遍历这棵树,p 指针和 q 指针一开始都指向这棵树的根,随后 p 右移时,q 左移,p 左移时,q 右移。每次检查当前 p 和 q 节点的值是否相等,如果相等再判断左右子树是否对称。
1
2
3
4
5
6
7
8
9
10
11
12
13
| public boolean isSymmetric(TreeNode root) {
return dfs(root, root);
}
public boolean dfs(TreeNode p, TreeNode q) {
if (p == null && q == null) {
return true;
}
if (p == null || q == null) {
return false;
}
return p.val == q.val && dfs(p.left, q.right) && dfs(p.right, q.left);
}
|
合并二叉树
617. 合并二叉树
问题
【LeetCode 617】:给你两棵二叉树: root1 和 root2,返回合并后的二叉树
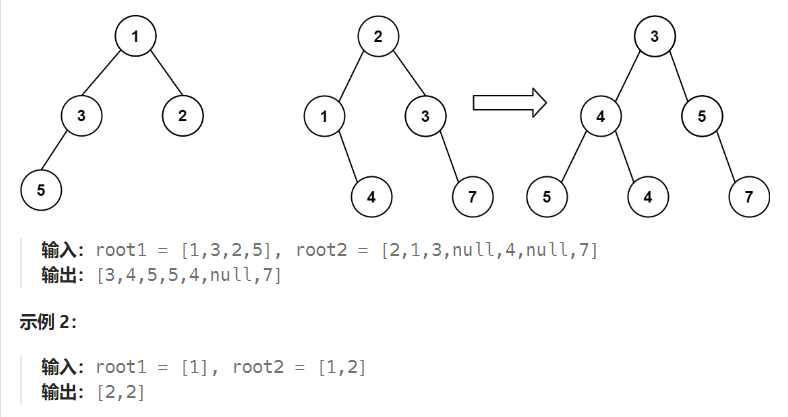
DFS
从根节点开始同时遍历两个二叉树,并将对应的节点进行合并:
- 如果两个二叉树的对应节点都为空,则合并后的二叉树的对应节点也为空;
- 如果两个二叉树的对应节点只有一个为空,则合并后的二叉树的对应节点为其中的非空节点;
- 如果两个二叉树的对应节点都不为空,则合并后的二叉树的对应节点的值为两个二叉树的对应节点的值之和,此时需要显性合并两个节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
return dfs(root1, root2);
}
public TreeNode dfs(TreeNode p, TreeNode q) {
if (p == null) {
return q;
}
if (q == null) {
return p;
}
TreeNode mergeNode = new TreeNode(p.val + q.val);
mergeNode.left = dfs(p.left, q.left);
mergeNode.right = dfs(p.right, q.right);
return mergeNode;
}
|
路径专题
二叉树的所有路径
257. 二叉树的所有路径
问题
【LeetCode 257】:给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径
DFS
在深度优先搜索遍历二叉树时,我们需要考虑当前的节点以及它的孩子节点。
- 如果当前节点不是叶子节点,则在当前的路径末尾添加该节点,并继续递归遍历该节点的每一个孩子节点。
- 如果当前节点是叶子节点,则在当前路径末尾添加该节点后我们就得到了一条从根节点到叶子节点的路径,将该路径加入到答案即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
public List<String> binaryTreePaths(TreeNode root) {
List<String> paths = new LinkedList<>();
dfs(root, "", paths);
return paths;
}
public void dfs(TreeNode node, String path, List<String> paths) {
if (node == null) {
return;
}
if (node.left == null && node.right == null) {
paths.add(path + node.val);
return;
}
dfs(node.left, path + node.val + "->", paths);
dfs(node.right, path + node.val + "->", paths);
}
|
路径总和
112. 路径总和
问题
【LeetCode 112】:给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
DFS
- 是否存在从当前节点
root 到叶子节点的路径,满足其路径和为 sum
- 假定从根节点到当前节点的值之和为
val,可以将这个大问题转化为一个小问题:是否存在从当前节点的子节点到叶子的路径,满足其路径和为 sum - val
- 不难发现这满足递归的性质,若当前节点就是叶子节点,那么我们直接判断
sum 是否等于 val
- 若当前节点不是叶子节点,只需要递归地询问它的子节点是否能满足条件即可
1
2
3
4
5
6
7
8
9
10
11
12
| public boolean hasPathSum(TreeNode root, int sum) {
if (root == null) {
return false;
}
if (root.left == null && root.right == null) {
return sum == root.val;
}
return hasPathSum(root.left, sum - root.val) ||
hasPathSum(root.right, sum - root.val);
}
|
翻转二叉树
226. 翻转二叉树
问题
【LeetCode 226】:给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
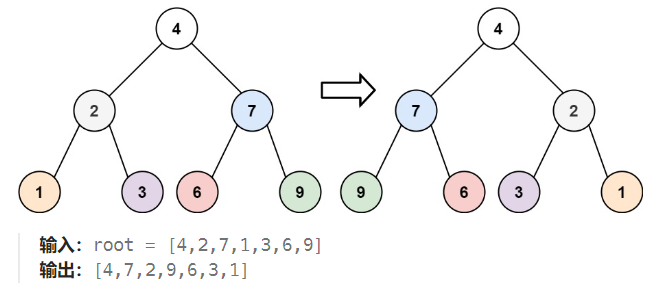
- 从根节点开始,递归地对树进行遍历,并从叶子节点先开始翻转
- 如果当前遍历到的节点
root 的左右两棵子树都已经翻转,那么只需要交换两棵子树的位置,即可完成以 root 为根节点的整棵子树的翻转
前序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
invertTree(root.left);
invertTree(root.right);
return root;
}
|
后序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
invertTree(root.left);
invertTree(root.right);
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
return root;
}
|
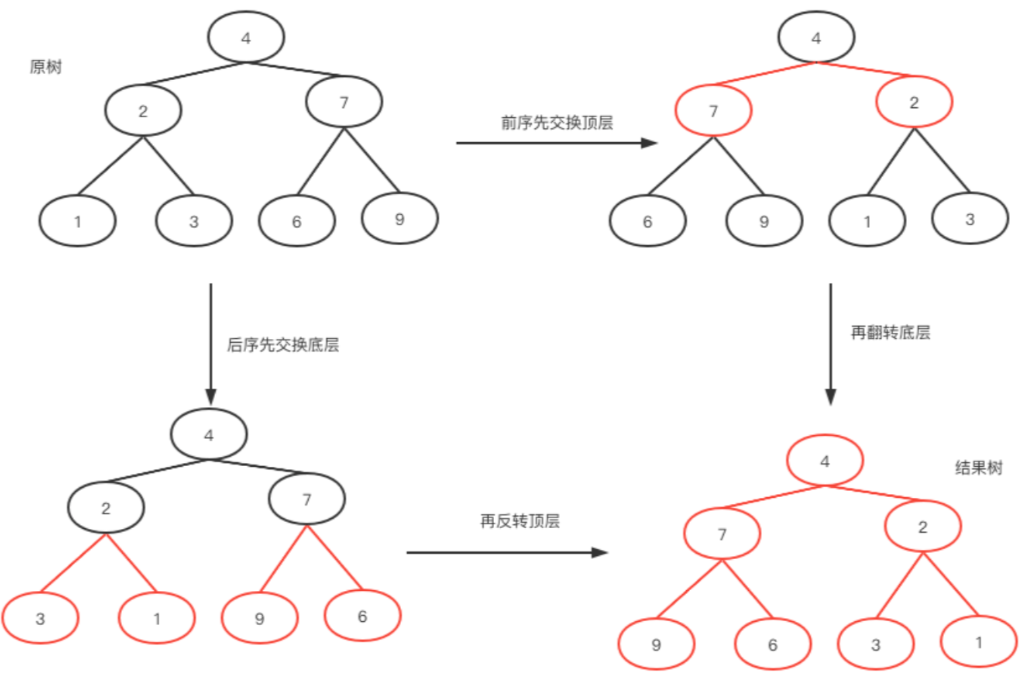
层次遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
Deque<TreeNode> deque = new LinkedList<>();
deque.offer(root);
while (deque.isEmpty()) {
TreeNode node = deque.poll();
TreeNode temp = node.left;
node.left = node.right;
node.right = temp;
if (node.left != null) {
deque.offer(node.left);
}
if (node.right != null) {
deque.offer(node.right);
}
}
return root;
}
|
二叉树 DFS 问题—高度和深度问题
通关进度
| 题目 |
说明 |
| 二叉树最大深度 |
通关 |
| 平衡二叉树 |
通关 |
| 二叉树最小深度 |
通关 |
| N 叉树最大深度 |
通关 |
二叉树最大深度
104. 二叉树的最大深度
问题
【LeetCode 104】:给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
DFS
如果左子树和右子树的最大深度 $l$ 和 $r$,那么该二叉树的最大深度即为:
1
2
3
4
5
6
7
8
9
10
| public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
} else {
int leftHeight = maxDepth(root.left);
int rightHeight = maxDepth(root.right);
return Math.max(leftHeight, rightHeight) + 1;
}
}
|
BFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int depth = 0;
while (!queue.isEmpty()) {
int levelSize = queue.size();
for (int i = 0; i < levelSize; i++) {
TreeNode node = queue.poll();
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
depth++;
}
return depth;
}
|
判断平衡树
110. 平衡二叉树
问题
【LeetCode 110】:给定一个二叉树,判断它是否是平衡二叉树
- 二叉树节点的高度:从该节点到叶子节点的最长简单路径边的条数
- 二叉树节点的深度:从根节点到该节点的最长简单路径边的条数
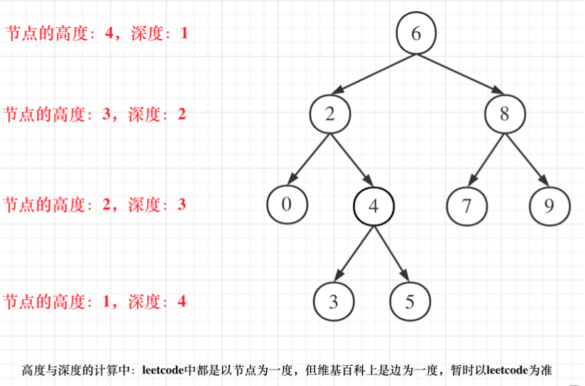
自底向上
- 采用后序遍历,对于当前遍历到的节点,先递归地判断其左右子树是否平衡,再判断以当前节点为根的子树是否平衡
- 如果一个子树平衡的,则返回其高度(高度一定是非负整数),否则返回 -1
如果存在一棵子树不平衡,则整个二叉树一定不平衡
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public boolean isBalanced(TreeNode root) {
return height(root) >= 0;
}
public int height(TreeNode node) {
if (node == null) {
return 0;
}
int leftHeight = height(node.left);
int rightHeight = height(node.right);
if (leftHeight == -1 || rightHeight == -1 || Math.abs(leftHeight - rightHeight) > 1) {
return -1;
} else {
return Math.max(leftHeight, rightHeight) + 1;
}
}
|
自顶向下
二叉树的前序遍历
- 对于当前遍历到的节点,首先计算左右子树的高度,如果左右子树的高度差是否不超过 1,再分别递归地遍历左右子节点,并判断左子树和右子树是否平衡
- 这是一个自顶向下的递归的过程。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
public boolean isBalanced(TreeNode root) {
if (root == null) {
return true;
} else {
return Math.abs(height(root.left) - height(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
}
}
public int height(TreeNode root) {
if (root == null) {
return 0;
} else {
return Math.max(height(root.left), height(root.right)) + 1;
}
}
|
最小深度
111. 二叉树的最小深度
问题
【LeetCode 111】:给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
DFS
- 使用深度优先搜索的方法,遍历整棵树,记录最小深度
- 对于每一个非叶子节点,只需要分别计算其左右子树的最小叶子节点深度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public int minDepth(TreeNode root) {
if (root == null) {
return 0;
}
if (root.left == null && root.right == null) {
return 1;
}
int min_depth = Integer.MAX_VALUE;
if (root.left != null) {
min_depth = Math.min(min_depth, minDepth(root.left));
}
if (root.right != null) {
min_depth = Math.min(min_depth, minDepth(root.right));
}
return min_depth + 1;
}
|
BFS
- 想到使用广度优先搜索的方法,遍历整棵树
- 一个叶子节点时,直接返回这个叶子节点的深度
- 当找到一个叶子节点时,直接返回这个叶子节点的深度
- 广度优先搜索的性质保证了最先搜索到的叶子节点的深度一定最小
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
class QueueNode {
TreeNode node;
int depth;
public QueueNode(TreeNode node, int depth) {
this.node = node;
this.depth = depth;
}
}
public int minDepth(TreeNode root) {
if (root == null) {
return 0;
}
Queue<QueueNode> queue = new LinkedList<>();
queue.offer(new QueueNode(root, 1));
while (!queue.isEmpty()) {
QueueNode nodeDepth = queue.poll();
TreeNode node = nodeDepth.node;
int depth = nodeDepth.depth;
if (node.left == null && node.right == null) {
return depth;
}
if (node.left != null) {
queue.offer(new QueueNode(node.left, depth + 1));
}
if (node.right != null) {
queue.offer(new QueueNode(node.right, depth + 1));
}
}
return 0;
}
|
N 叉树最大深度
559. N 叉树的最大深度
问题
【LeetCode 559】:给定一个 N 叉树,找到其最大深度。
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
DFS
如果根节点有 N 个子节点,则这 N 个子节点对应 N 个子树。记 N 个子树的最大深度中的最大值为 maxChildDepth,则该 N 叉树的最大深度为 maxChildDepth + 1。
在计算当前 N 叉树的最大深度时,可以先递归计算出其每个子树的最大深度,然后在 $O(1)$ 的时间内计算出当前 N 叉树的最大深度。递归在访问到空节点时退出。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
public int maxDepth(Node root) {
if (root == null) {
return 0;
}
int maxChildDepth = 0;
List<Node> children = root.children;
for (Node child : children) {
int childDepth = maxDepth(child);
maxChildDepth = Math.max(maxChildDepth, childDepth);
}
return maxChildDepth + 1;
}
|
BFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
public int maxDepth(Node root) {
if (root == null) {
return 0;
}
Queue<Node> queue = new LinkedList<Node>();
queue.offer(root);
int depth = 0;
while (!queue.isEmpty()) {
int levelSize = queue.size();
for (int i = 0; i < levelSize; i++) {
Node node = queue.poll();
List<Node> children = node.children;
for (Node child : children) {
queue.offer(child);
}
}
depth++;
}
return depth;
}
|
二叉树 DFS 问题—祖先问题
通关进度
最近公共祖先问题
236. 二叉树的最近公共祖先
问题
【LeetCode 236】:给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
哈希
- 从根节点开始遍历整棵二叉树,用哈希表记录每个节点的父节点指针
- 从
p 节点开始不断往它的祖先移动,并用数据结构记录已经访问过的祖先节点
- 同样再从
q 节点开始不断往它的祖先移动,如果有祖先已经被访问过,即意味着这是 p 和 q 的深度最深的公共祖先,即 LCA 节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| Map<Integer, TreeNode> parent = new HashMap<>();
Set<Integer> visited = new HashSet<>();
public void dfs(TreeNode root) {
if (root.left != null) {
parent.put(root.left.val, root);
dfs(root.left);
}
if (root.right != null) {
parent.put(root.right.val, root);
dfs(root.right);
}
}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
dfs(root);
while (p != null) {
visited.add(p.val);
p = parent.get(p.val);
}
while (q != null) {
if (visited.contains(q.val)) {
return q;
}
q = parent.get(q.val);
}
return null;
}
|
DFS
后序遍历二叉树,当前节点记为 cur,假设处理 cur 左子树返回节点为 left,处理右子树时返回节点为 right
- 如果发现
cur 等于 null,或者 o1、o2,则返回 cur
- 如果
left 和 right 都为空,说明 cur 整棵子树没有发现过 o1 或 o2,返回 null
- 如果
left 和 S 都不为空,说明左子树发现过 o1 或 o2,右子树也发现过 o1 或 o2,说明 o1 向上与 o2 向上的过程中,首次在 cur 相遇,返回 cur
- 如果
left 和 right 有一个为空,另一个不为空,假设不为空的那个记为 node,此时 node 要么是 o1 或 o2 的一个,要么是 o1 和 o2 的最近公共祖先,直接返回 node
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| public TreeNode lowestCommonAncestor(TreeNode root, TreeNode o1, TreeNode o2) {
if (root == null || root == o1 || root == o2) {
return root;
}
TreeNode left = lowestCommonAncestor(root.left, o1, o2);
TreeNode right = lowestCommonAncestor(root.right, o1, o2);
if (left != null && right != null) {
return root;
}
return left != null ? left : right;
}
|
















