快速排序
参考资料
全网最好懂的快速排序的原理
基本思想
通过枢轴将元素序列划分成左右两个子序列 left 和 right,其中 left 比枢轴小,right 比枢轴大,然后再对枢轴左右两侧递归执行快速排序
荷兰旗思路
quickSort
1 2 3 4 5 6 public void quickSort (int [] arr) { if (arr == null || arr.length < 2 ) { return ; } quickSort(arr, 0 , arr.length - 1 ); }
1 2 3 4 5 6 7 8 9 10 public void quickSort (int [] arr, int left, int right) { if (left < right) { swap(arr, left + (int )(Math.random() * (right - left + 1 )), right); int [] p = partition(arr, left, right); quickSort(arr, left, p[0 ] - 1 ); quickSort(arr, p[1 ] + 1 , right); } }
partition
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 public int [] partition(int [] arr, int left, int right) { int lessZoneRightBoundary = left - 1 ; int moreZoneLeftBoundary = right + 1 ; while (left < moreZoneLeftBoundary) { if (arr[left] < arr[right]) { swap(arr, ++lessZoneRightBoundary, left++); } else if (arr[left] > arr[right]) { swap(arr, --moreZoneLeftBoundary, left); } else { left++; } } return new int [] {lessZoneRightBoundary + 1 , moreZoneLeftBoundary - 1 }; }
一般思路 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 public void quickSort (int [] array, int start, int end) { if (start >= end) { return ; } int pivotIndex = doublePointerSwap(array, start, end); quickSort(array, start, pivotIndex - 1 ); quickSort(array, pivotIndex + 1 , end); } public int doublePointerSwap (int [] arr, int startIndex, int endIndex) { int pivot = arr[startIndex]; int leftPoint = startIndex; int rightPoint = endIndex; while (leftPoint < rightPoint) { while (leftPoint < rightPoint && arr[rightPoint] > pivot) { rightPoint--; } while (leftPoint < rightPoint && arr[leftPoint] <= pivot) { leftPoint++; } if (leftPoint < rightPoint) { int temp = arr[leftPoint]; arr[leftPoint] = arr[rightPoint]; arr[rightPoint] = temp; } } arr[startIndex] = arr[rightPoint]; arr[rightPoint] = pivot; return rightPoint; }
数组中第 K 大的值 215. 数组中的第K个最大元素
问题
【LeetCode 215】:给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
基于快速排序的选择方法 选取 pivot,把小于 pivot 的元素都移到 pivot 之前,这样 pivot 所在位置就是第 pivot index 小的元素。
只要找到当前 pivot 的位置是否是在第 $n-k$ 小的位置,如果是,找到第 $k$ 大的数直接返回。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 public int findKthLargest (int [] _nums, int k) { return search(_nums, 0 , _nums.length - 1 , _nums.length - k); } public int search (int [] nums, int begin, int end, int k) { int pivotIndex = partition(nums, begin, end); if (pivotIndex == k) { return nums[pivotIndex]; } else if (pivotIndex > k) { return search(nums, begin, pivotIndex - 1 , k); } else { return search(nums, pivotIndex + 1 , end, k); } } public int partition (int [] nums, int startIndex, int endIndex) { int pivot = nums[startIndex]; int leftPoint = startIndex; int rightPoint = endIndex; while (leftPoint < rightPoint) { while (leftPoint < rightPoint && nums[rightPoint] > pivot) { rightPoint--; } while (leftPoint < rightPoint && nums[leftPoint] <= pivot) { leftPoint++; } if (leftPoint < rightPoint) { int temp = nums[leftPoint]; nums[leftPoint] = nums[rightPoint]; nums[rightPoint] = temp; } } nums[startIndex] = nums[rightPoint]; nums[rightPoint] = pivot; return rightPoint; }
基于堆排序的选择方法 使用大根堆做 k−1 次删除操作后堆顶元素
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 public int findKthLargest (int [] nums, int k) { int heapSize = nums.length; buildMaxHeap(nums, heapSize); for (int i = nums.length - 1 ; i >= nums.length - k + 1 ; --i) { swap(nums, 0 , i); --heapSize; maxHeapify(nums, 0 , heapSize); } return nums[0 ]; } public void buildMaxHeap (int [] a, int heapSize) { for (int i = heapSize / 2 ; i >= 0 ; --i) { maxHeapify(a, i, heapSize); } } public void maxHeapify (int [] a, int i, int heapSize) { int l = i * 2 + 1 , r = i * 2 + 2 , largest = i; if (l < heapSize && a[l] > a[largest]) { largest = l; } if (r < heapSize && a[r] > a[largest]) { largest = r; } if (largest != i) { swap(a, i, largest); maxHeapify(a, largest, heapSize); } } public void swap (int [] a, int i, int j) { int temp = a[i]; a[i] = a[j]; a[j] = temp; }
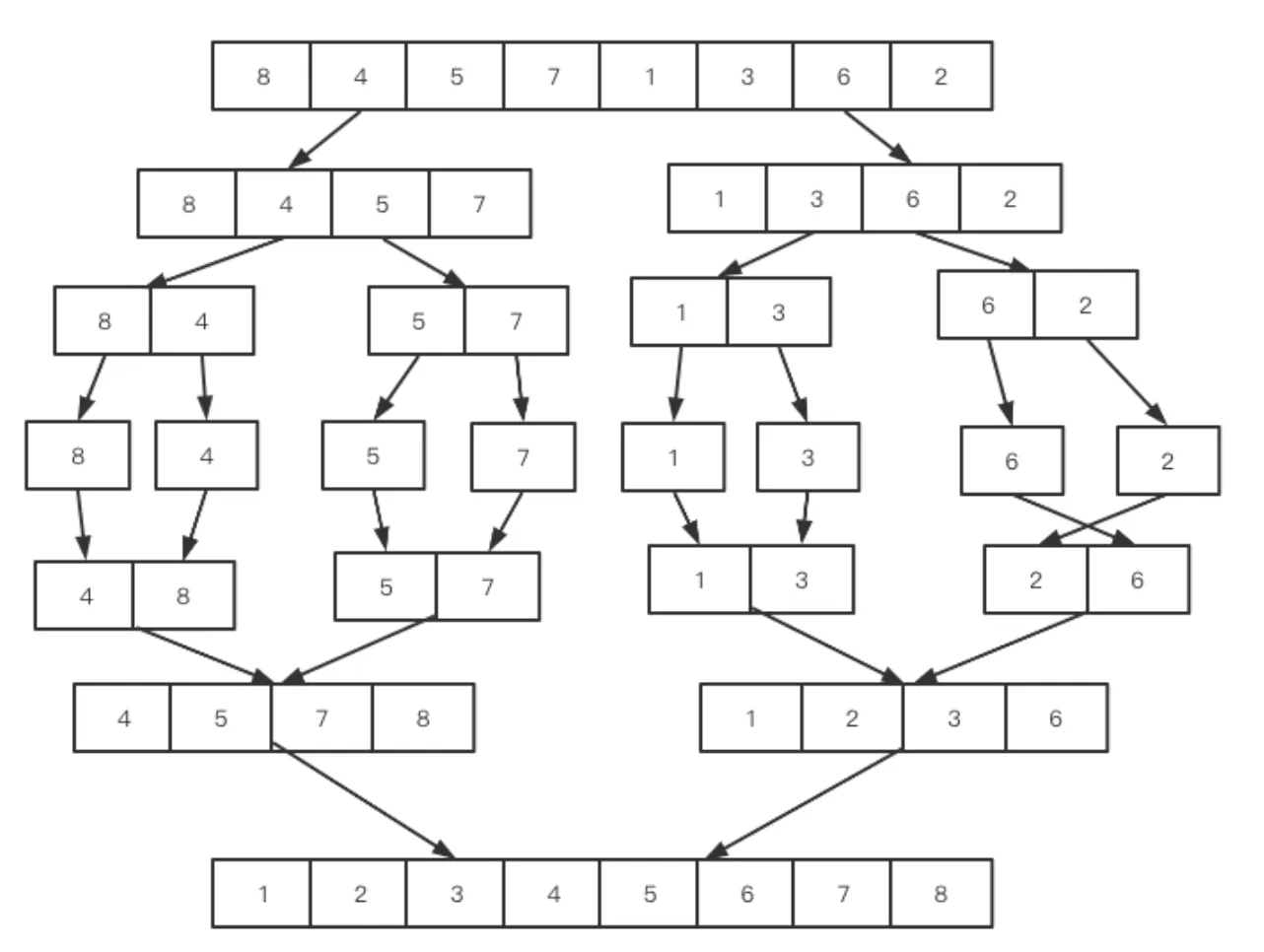
归并排序
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 public void merge (int [] arr, int left, int mid, int right) { int [] temp = new int [right - left + 1 ]; int i = 0 ; int p1 = left; int p2 = mid + 1 ; while (p1 <= mid && p2 <= right) { temp[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++]; } while (p1 <= mid) { temp[i++] = arr[p1++]; } while (p2 <= right) { temp[i++] = arr[p2++]; } for (int j = 0 ; j < temp.length ; j++) { arr[left + j] = temp[j]; } } public void mergeSort (int [] arr, int left, int right) { if (left == right) { return ; } int mid = left + ((right - left) >> 1 ); mergeSort(arr, left, mid); mergeSort(arr, mid + 1 , right); merge(arr, left, mid, right); } public void mergeSort (int [] arr) { if (arr == null || arr.length < 2 ) { return ; } mergeSort(arr, 0 , arr.length - 1 ); }