数字与数学基础问题
通关进度
| 题目 |
说明 |
| 数字统计 |
通关 |
| 数字溢出 |
通关 |
| 进制处理 |
通关 |
数字统计专题
数组元素积的符号
1822. 数组元素积的符号
问题
【LeetCode 1822】:已知函数 signFunc(x) 将会根据 x 的正负返回特定值:
- 如果
x 是正数,返回 1 。
- 如果
x 是负数,返回 -1 。
- 如果
x 是等于 0 ,返回 0 。
给你一个整数数组 nums 。令 product 为数组 nums 中所有元素值的乘积。
返回 signFunc(product) 。
遍历
- 如果数组中有一个元素
0,那么所有元素值的乘积肯定为 0,我们直接返回 0
- 使用
sign 记录元素值乘积的符号,1 为表示正,−1 表示为负,初始时 sign=1
- 遍历整个数组,如果元素为正,那么
sign 不变,否则令 sign=−sign,最后返回 sign
1
2
3
4
5
6
7
8
9
10
11
12
| public int arraySign(int[] nums) {
int sign = 1;
for (int num : nums) {
if (num == 0) {
return 0;
}
if (num < 0) {
sign = -sign;
}
}
return sign;
}
|
阶乘尾数
面试题 16.05. 阶乘尾数
问题
【面试题 16.05】:设计一个算法,算出 n 阶乘有多少个尾随零。
算法思路
$0$ 的产生需要 $5 \times 2$, 所以题目目标转换为求 Min{count_5,count_2}, 但 2 出现的数量明显大于 5 ,所以实际上题目的目标就是求 5 出现的次数
1
2
3
4
5
6
7
8
9
|
public int trailingZeroes(int n) {
int ans = 0;
while (n != 0) {
n /= 5;
ans += n;
}
return ans;
}
|
数字溢出专题
整数反转
7. 整数反转
问题
【LeetCode 7】:给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果
反转处理
1
2
3
4
5
6
|
digit = x % 10
x /= 10
rev = rev * 10 + digit
|
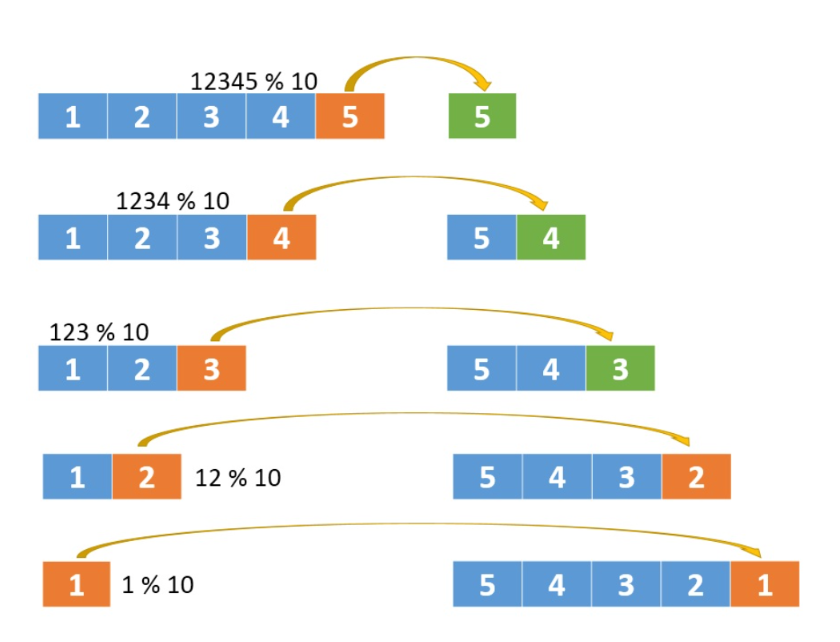
溢出处理
在「推入」数字之前,判断是否满足,若该不等式不成立则返回 $0$,证明过程

1
2
3
4
5
6
7
8
9
10
11
12
13
| public int reverse(int x) {
int rev = 0;
while (x != 0) {
if (rev < Integer.MIN_VALUE / 10 || rev > Integer.MAX_VALUE / 10) {
return 0;
}
int digit = x % 10;
x /= 10;
rev = rev * 10 + digit;
}
return rev;
}
|
字符串转整数
参考 字符串专题
回文数
9. 回文数
问题
【LeetCode 9】:给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。
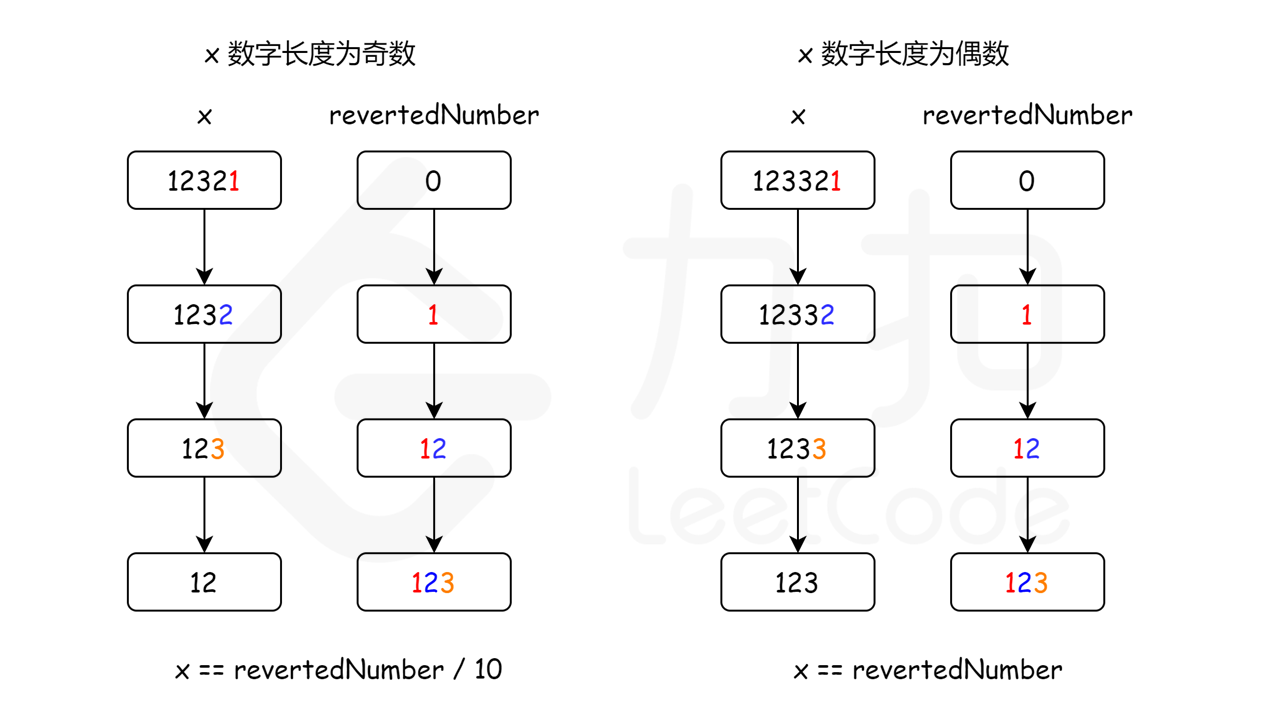
反转一半数字
- 反转一半数字,与前半段进行比较判断回文,避免溢出
- 负数一律不满足条件,直接过滤
- 由于整个过程不断将原始数字除以
10,然后给反转后的数字乘上 10
- 因此当原始数字小于或等于反转后的数字时,就意味着我们已经处理了一半位数的数字
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| public boolean isPalindrome(int x) {
if (x < 0 || (x % 10 == 0 && x != 0)) {
return false;
}
int revertedNumber = 0;
while (x > revertedNumber) {
revertedNumber = revertedNumber * 10 + x % 10;
x /= 10;
}
return x == revertedNumber || x == revertedNumber / 10;
}
|
进制处理专题
七进制数
504. 七进制数
问题
【LeetCode 504】:给定一个整数 num,将其转化为 7 进制,并以字符串形式输出。
进制转换

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public String convertToBase7(int num) {
if (num == 0) {
return "0";
}
boolean negative = num < 0;
num = Math.abs(num);
StringBuffer digits = new StringBuffer();
while (num > 0) {
digits.append(num % 7);
num /= 7;
}
if (negative) {
digits.append('-');
}
return digits.reverse().toString();
}
|
进制转换
问题
给定十进制 $M$,以及需要转换的进制数 $N$,将十进制数 $M$ 转换成 $N$ 进制数,其中 $M$ 是 32 位整数,$2\le{N}\le{16}$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public static final String[] base = {
"0", "1", "2", "3", "4", "5", "6", "7", "8", "9"
, "A", "B", "C", "D", "E", "F"};
public String convertToBaseN(int m, int n) {
if (m == 0) {
return "0";
}
boolean negative = m < 0;
m = Math.abs(m);
StringBuffer digits = new StringBuffer();
while (m > 0) {
digits.append(base[m % n]);
m /= n;
}
if (negative) {
digits.append('-');
}
return digits.reverse().toString();
}
|
数字与数学高频问题
通关进度
数组实现加法专题
数组实现整数加法
66. 加一
问题
【LeetCode 66】:给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。
最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。
算法思想
当对数组 digits 加一时,只需要关注 digits 的末尾出现了多少个 9 即可
- 如果
digits 的末尾没有 9,例如 [1,2,3],那么直接将末尾的数加一,得到 [1,2,4] 并返回;
- 如果
digits 的末尾有若干个 9,例如 [1,2,3,9,9],那么只需要找出从末尾开始的第一个不为 9 的元素,即 3,将该元素加一,得到 [1,2,4,9,9]。随后将末尾的 9 全部置零,得到 [1,2,4,0,0] 并返回
- 如果
digits 的所有元素都是 9,例如 [9,9,9,9,9],那么答案为 [1,0,0,0,0,0]。只需要构造一个长度比 digits 多 1 的新数组,将首元素置为 1,其余元素置为 0 即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| public int[] plusOne(int[] digits) {
int n = digits.length;
for (int i = n - 1; i >= 0; --i) {
if (digits[i] != 9) {
++digits[i];
for (int j = i + 1; j < n; ++j) {
digits[j] = 0;
}
return digits;
}
}
int[] ans = new int[n + 1];
ans[0] = 1;
return ans;
}
|
字符串加法
问题
给定两个字符串形式的非负整数 num1 和 num1,以字符串形式返回两数之和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
public String addStrings(String num1, String num2) {
int i = num1.length() - 1, j = num2.length() - 1;
int adder = 0;
StringBuilder sb = new StringBuilder();
while (i >= 0 || j >= 0 || adder != 0) {
int x = i >= 0 ? num1.charAt(i) - '0' : 0;
int y = j >= 0 ? num1.charAt(j) - '0' : 0;
int sum = x + y + adder;
sb.append(sum % 10);
adder = sum / 10;
i--;
j--;
}
return sb.reverse().toString();
}
|
二进制加法
67. 二进制求和
问题
【LeetCode 67】:给你两个二进制字符串 a 和 b ,以二进制字符串的形式返回它们的和
模拟
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public String addBinary(String a, String b) {
StringBuffer ans = new StringBuffer();
int n = Math.max(a.length(), b.length()), carry = 0;
for (int i = 0; i < n; ++i) {
carry += i < a.length() ? (a.charAt(a.length() - 1 - i) - '0') : 0;
carry += i < b.length() ? (b.charAt(b.length() - 1 - i) - '0') : 0;
ans.append((char) (carry % 2 + '0'));
carry /= 2;
}
if (carry > 0) {
ans.append('1');
}
ans.reverse();
return ans.toString();
}
|
位运算
幂运算专题
求 2 的幂
231. 2 的幂
问题
【LeetCode 231】:给你一个整数 n,请你判断该整数是否是 2 的幂次方。如果是,返回 true ;否则,返回 false
试除法
- 如果 $n$ 是 $2$ 的幂,则 $n>0$,且存在非负整数 $k$ 使得 $n=2^k$
- 首先判断 $n$ 是不是正整数,如果 $n$ 是 $0$ 或负整数,则 $n$ 一定不是 $2$ 的幂
- 当 $n$ 是正整数时,为判断 $n$ 是否是 $2$ 的幂,可以连续对 $n$ 进行除以 $2$ 的操作,直到 $n$ 不能被 $2$ 整除。此时如果 $n=1$,则 $n$ 是 $2$ 的幂,否则 $n$ 不是 $2$ 的幂
1
2
3
4
5
6
7
8
9
10
| public boolean isPowerOfTwo(int n) {
if (n <= 0) {
return false;
}
while (n % 2 == 0) {
n /= 2;
}
return n == 1;
}
|
二进制表示:
一个数 $n$ 是 $2$ 的幂,当且仅当 $n$ 是正整数,并且 $n$ 的二进制表示中仅包含 $1$ 个 $1$ , 可以考虑使用位运算,将 $n$ 的二进制表示中最低位的那个 $1$ 提取出来,再判断剩余的数值是否为 $0$ 即可
二进制表示中最低位 — $n \& (n - 1) $

1
2
3
| public boolean isPowerOfTwo(int n) {
return n > 0 && (n & (n - 1)) == 0;
}
|
二进制表示中最低位 — $ n \& (-n) $

1
2
3
| public boolean isPowerOfTwo(int n) {
return n > 0 && (n & -n) == n;
}
|
求 3 的幂
326. 3 的幂
问题
给定一个整数,写一个函数来判断它是否是 3 的幂次方。如果是,返回 true ;否则,返回 false 。
整数 n 是 3 的幂次方需满足:存在整数 x 使得 n == 3^x
试除法
- 不断地将 $n$ 除以 $3$,直到 $n=1$。如果此过程中 $n$ 无法被 $3$ 整除,就说明 $n$ 不是 $3$ 的幂
- 如果 $n$ 是 $3$ 的幂,则 $n>0$,且存在非负整数 $k$ 使得 $n=3^k$
- 首先判断 $n$ 是不是正整数,如果 $n$ 是 $0$ 或负整数,则 $n$ 一定不是 $3$ 的幂
- 当 $n$ 是正整数时,为判断 $n$ 是否是 $3$ 的幂,可以连续对 $n$ 进行除以 $3$ 的操作,直到 $n$ 不能被 $3$ 整除。此时如果 $n=1$,则 $n$ 是 $3$ 的幂,否则 $n$ 不是 $3$ 的幂
1
2
3
4
5
6
7
8
9
| public boolean isPowerOfThree(int n) {
if (n <= 0) {
return false;
}
while (n % 3 == 0) {
n /= 3;
}
return n == 1;
}
|
参考答案
求 4 的幂
342. 4的幂
问题
给定一个整数,写一个函数来判断它是否是 4 的幂次方。如果是,返回 true ;否则,返回 false 。
整数 n 是 4 的幂次方需满足:存在整数 x 使得 n == 4^x
试除法
1
2
3
4
5
6
7
8
9
10
| public boolean isPowerOfFour(int n) {
if (n <= 0) {
return false;
}
while (n % 4 == 0) {
n /= 4;
}
return n == 1;
}
|
转化为 2 的幂求解
一个数 $n$ 如果是 $4$ 的幂,等价于 $n$ 为质因数只有 $2$ 的平方数。因此可以将问题其转换:判断 $\sqrt{n}$
是否为 $2$ 的幂。
1
2
3
4
5
6
| public boolean isPowerOfFour(int n) {
if (n <= 0) return false;
int x = (int)Math.sqrt(n);
return x * x == n && (x & -x) == x;
}
|
x 的幂
50. Pow(x, n)
问题
实现 pow(x, n) ,即计算 x 的整数 n 次幂函数
快速幂 + 递归

1
2
3
4
5
6
7
8
9
10
11
12
| public double myPow(double x, int n) {
long N = n;
return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
}
public double quickMul(double x, long N) {
if (N == 0) {
return 1.0;
}
double y = quickMul(x, N / 2);
return N % 2 == 0 ? y * y : y * y * x;
}
|
快速幂 + 迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| public double myPow(double x, int n) {
long N = n;
return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
}
public double quickMul(double x, long N) {
double ans = 1.0;
double x_contribute = x;
while (N > 0) {
if (N % 2 == 1) {
ans *= x_contribute;
}
x_contribute *= x_contribute;
N /= 2;
}
return ans;
}
|
数论问题
通关进度
| 题目 |
说明 |
| 最大公约数 |
通关 |
| 素数和合数 |
通关 |
| 埃氏筛 |
通关 |
| 丑数问题 |
通关 |
最大公约数
辗转相除法
若 $r$ 是 $a÷b$ 的余数,则 $gcd(a,b)=gcd(b,r)$。如何证明辗转相除法(欧几里德算法)?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public int gcd(int a, int b) {
int k = 0;
do {
k = a % b;
a = b;
b = k;
} while (k != 0);
return a;
}
|
最小公倍数
1
| lcm(a, b) = (a * b)/gcd(a, b)
|
素数和合数
素数
素数满足大于等于 $2$,并且除了 $1$ 和它本身之外,不能被其他任何自然数整除,其他都是合数。
- 1 既非素数,也非合数
- 2 是唯一的同时为偶数和素数的数字
1
2
3
4
5
6
7
8
9
10
| public boolean isPrime(int num) {
int max = (int) Math.sqrt(num);
for (int i = 2; i <= max; i++) {
if (num % i == 0) {
return false;
}
}
return true;
}
|
204. 计数质数
1
2
3
4
5
6
7
8
9
| public int countPrimes(int n) {
int cnt = 0;
for (int i = 2; i < n; i++) {
if (isPrime(i)) {
cnt++;
}
}
return cnt;
}
|
埃氏筛
204. 计数质数
问题
给定整数 n ,返回所有小于非负整数 n 的质数的数量
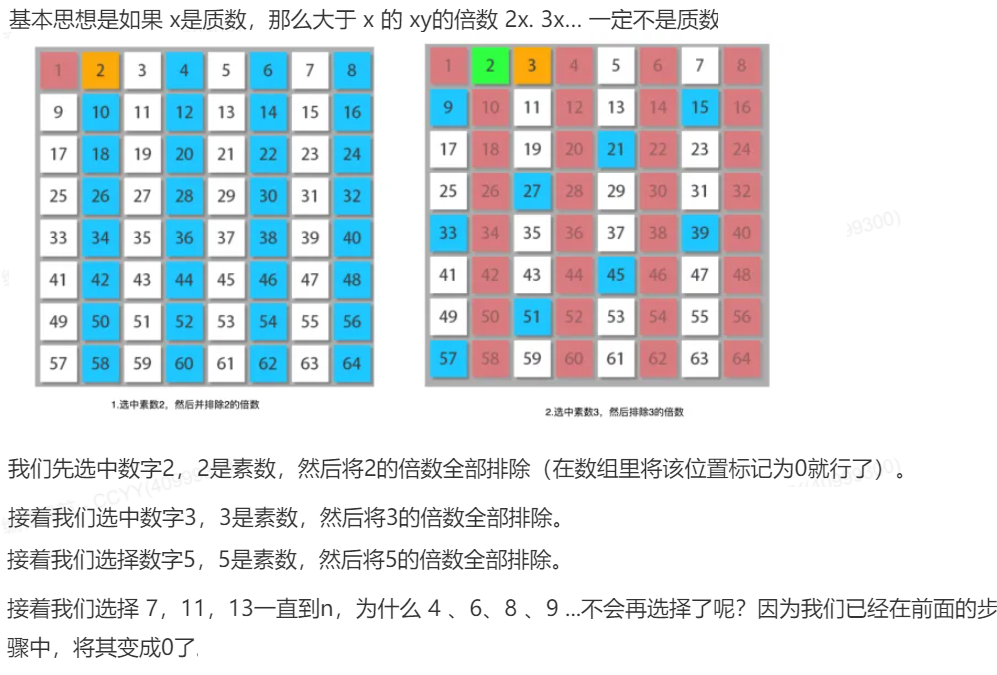
埃氏筛

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| public int countPrimes(int n) {
int[] isPrime = new int[n];
Arrays.fill(isPrime, 1);
int ans = 0;
for (int i = 2; i < n; ++i) {
if (isPrime[i] == 1) {
ans += 1;
if ((long) i * i < n) {
for (int j = i * i; j < n; j += i) {
isPrime[j] = 0;
}
}
}
}
return ans;
}
|
丑数问题
LCR 168. 丑数
问题
给你一个整数 n ,请你找出并返回第 n 个 丑数 。
说明:丑数是只包含质因数 2、3 和/或 5 的正整数;1 是丑数。
数学

1
2
3
4
5
6
7
8
9
10
11
12
| public boolean isUgly(int n) {
if (n <= 0) {
return false;
}
int[] factors = {2, 3, 5};
for (int factor : factors) {
while (n % factor == 0) {
n /= factor;
}
}
return n == 1;
}
|
最小堆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public int nthUglyNumber(int n) {
int[] factors = {2, 3, 5};
Set<Long> seen = new HashSet<Long>();
PriorityQueue<Long> heap = new PriorityQueue<Long>();
seen.add(1L);
heap.offer(1L);
int ugly = 0;
for (int i = 0; i < n; i++) {
long curr = heap.poll();
ugly = (int) curr;
for (int factor : factors) {
long next = curr * factor;
if (seen.add(next)) {
heap.offer(next);
}
}
}
return ugly;
}
|





















