堆结构
通关进度
| 题目 |
说明 |
| 构造堆 |
通关 |
| 添加堆元素 |
通关 |
| 删除堆元素 |
通关 |
参考资料
应该是全网最详细的解释算法里堆的课时
堆
堆中的每一个节点值都大于等于(或小于等于)子树中所有节点的值。或者说,任意一个节点的值都大于等于(或小于等于)所有子节点的值
- 最大堆:堆中的每一个节点的值都大于等于子树中所有节点的值
- 最小堆:堆中的每一个节点的值都小于等于子树中所有节点的值
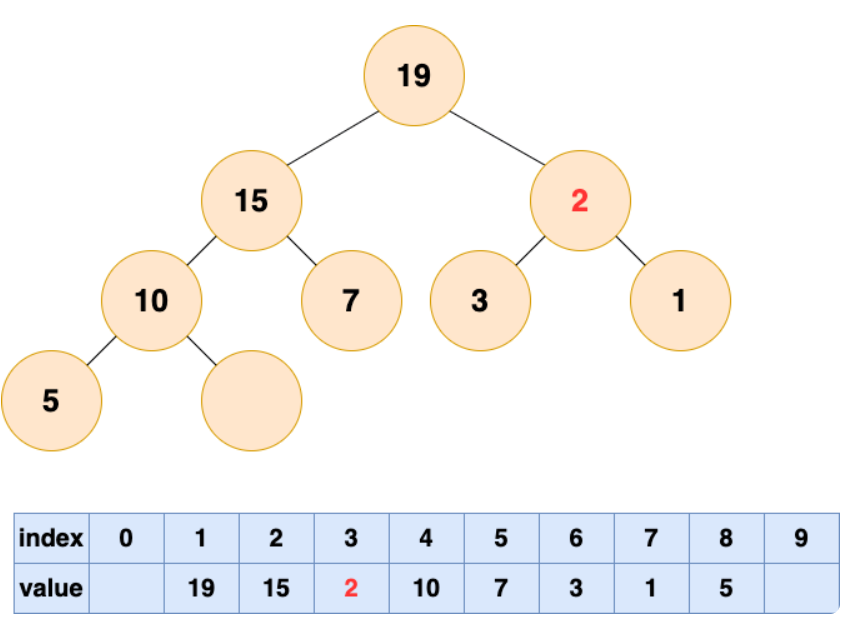
堆的存储
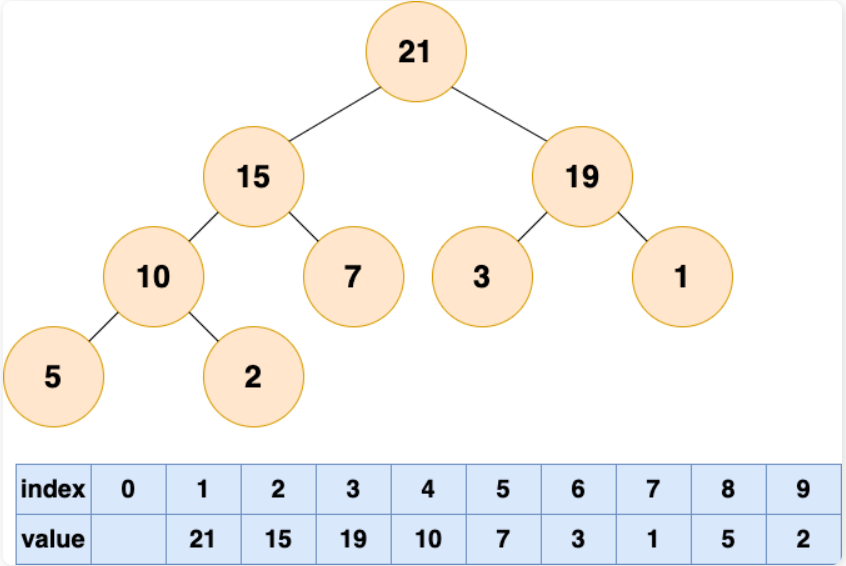
堆的插入
1.将要插入的元素放到最后
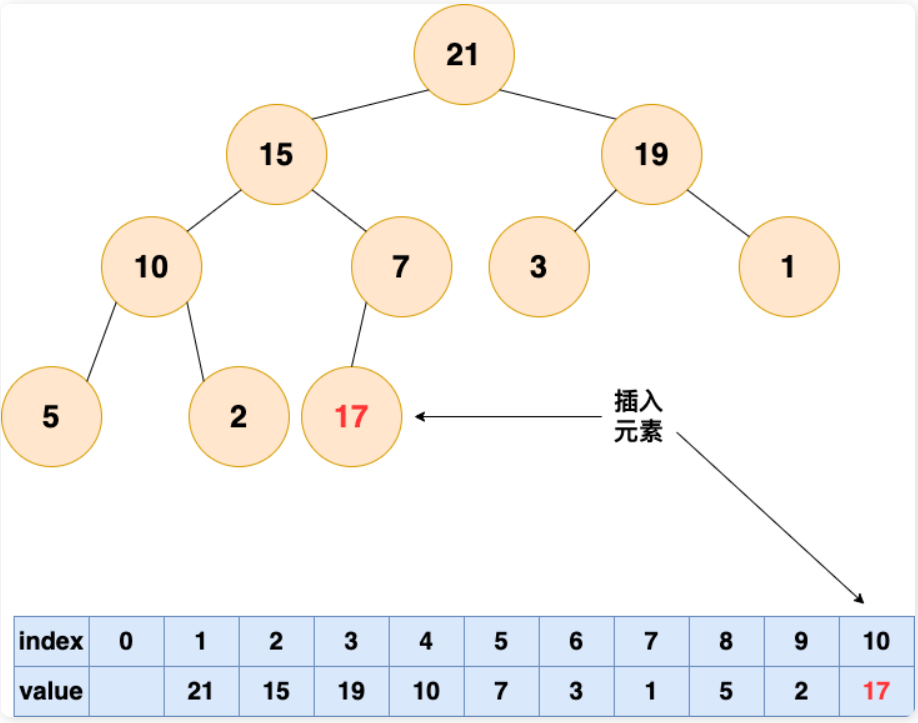
2.从底向上,如果父结点比该元素小,则该节点和父结点交换,直到无法交换
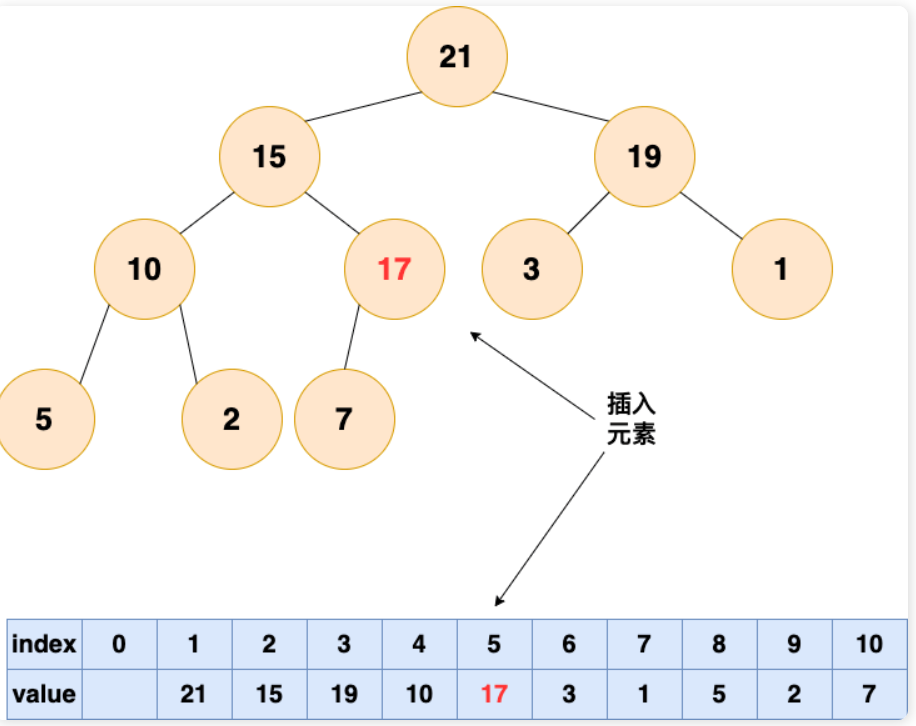
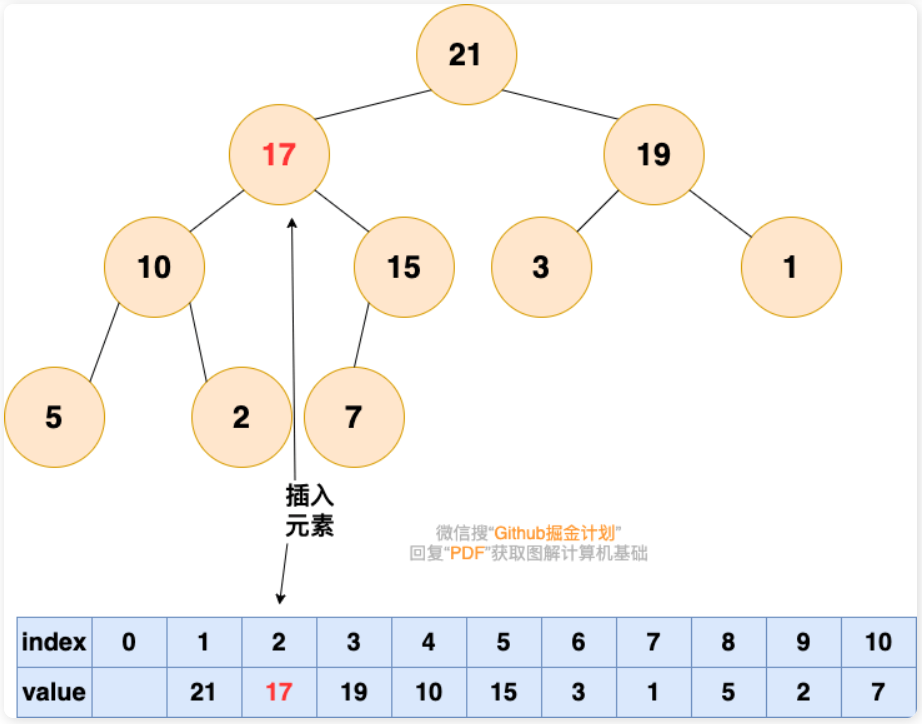
堆的删除
根据堆的性质可知,最大堆的堆顶元素为所有元素中最大的,最小堆的堆顶元素是所有元素中最小的。当我们需要多次查找最大元素或者最小元素的时候,可以利用堆来实现。
删除堆顶元素后,为保持堆的性质,需要对堆的结构进行调整,我们将这个过程称之为”堆化”,堆化的方法分为两种:
- 一种是自底向上的堆化,上述的插入元素所使用的就是自底向上的堆化,元素从最底部向上移动。
- 另一种是自顶向下堆化,元素由最顶部向下移动
自底向上堆化
首先删除堆顶元素,使得数组中下标为 1 的位置空出。
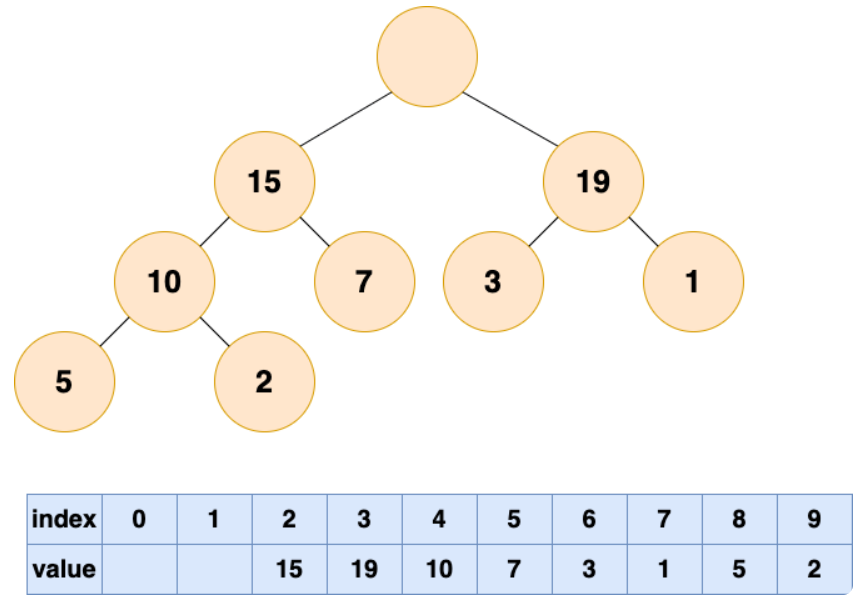
比较根结点的左子节点和右子节点,也就是下标为 2,3 的数组元素,将较大的元素填充到根结点(下标为 1)的位置。
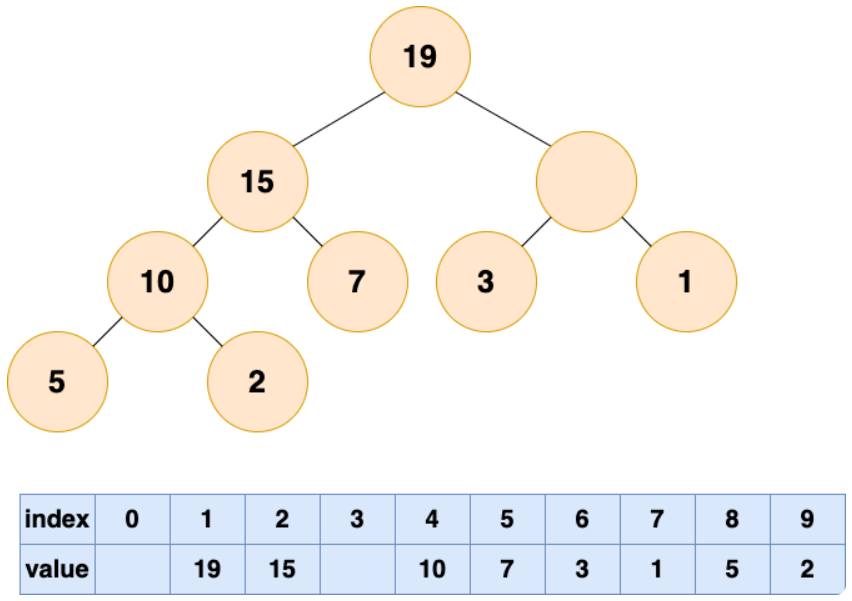
一直循环比较空出位置的左右子节点,并将较大者移至空位,直到堆的最底部
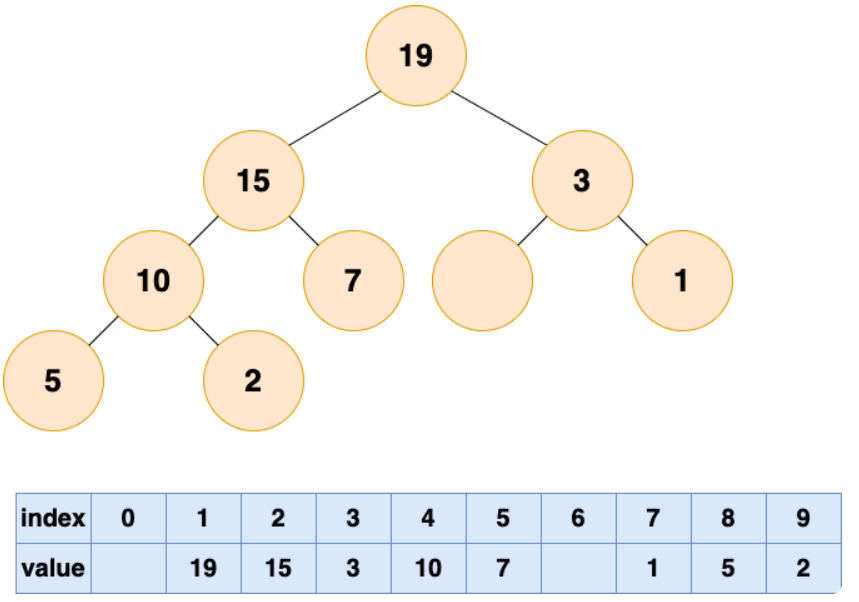
自顶向下堆化
自顶向下的堆化用一个词形容就是“石沉大海”,那么第一件事情,就是把石头抬起来,从海面扔下去。这个石头就是堆的最后一个元素,我们将最后一个元素移动到堆顶。
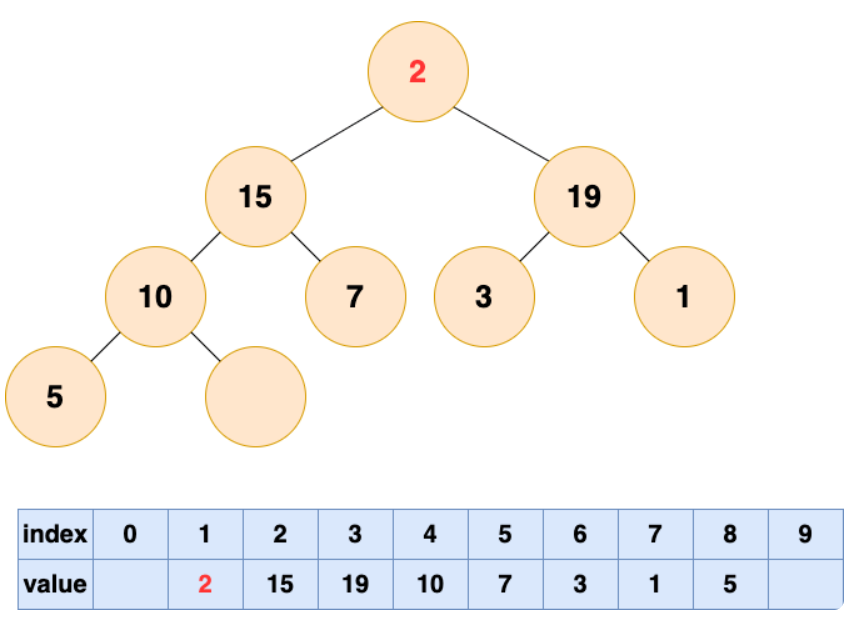
然后开始将这个石头沉入海底,不停与左右子节点的值进行比较,和较大的子节点交换位置,直到无法交换位置。

堆经典问题
通关进度
| 题目 |
说明 |
| 堆排序 |
通关 |
| 数组中第 K 大的元素 |
通关 |
| 合并 K 个排序链表 |
通关 |
堆排序
堆排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| public void heapSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
for (int i = 0; i < arr.length; i++) {
heapInsert(arr, i);
}
int size = arr.length;
swap(arr, 0, --size);
while (size > 0) {
heapify(arr, 0, size);
swap(arr, 0, --size);
}
}
|
堆的插入
1
2
3
4
5
6
7
8
9
10
11
|
public void heapInsert(int[] arr, int index) {
while (arr[index] > arr[index - 1] / 2) {
int temp = arr[index];
arr[index] = arr[(index - 1) / 2];
arr[(index - 1) / 2] = temp;
index = (index - 1) / 2;
}
}
|
堆的调整
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
public void heapify(int[] arr, int index, int size) {
int left = index * 2 + 1;
while (left < size) {
int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;
largest = arr[largest] > arr[index] ? largest : index;
if (largest == index) {
break;
}
int temp = arr[index];
arr[index] = arr[largest];
arr[largest] = temp;
index = largest;
left = index * 2 + 1;
}
}
|
数组中第 K 大的元素
215. 数组中的第K个最大元素
问题
【LeetCode 215】:给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
算法思想
建立一个大根堆,做 k−1 次删除操作后堆顶元素就是我们要找的答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| public int findKthLargest(int[] nums, int k) {
int heapSize = nums.length;
buildMaxHeap(nums, heapSize);
for (int i = nums.length - 1; i >= nums.length - k + 1; --i) {
swap(nums, 0, i);
--heapSize;
heapify(nums, 0, heapSize);
}
return nums[0];
}
public void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
public void buildMaxHeap(int[] arr, int heapSize) {
for (int i = heapSize / 2; i >= 0; --i) {
heapify(arr, i, heapSize);
}
}
|
堆化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
public void heapify(int[] arr, int index, int size) {
int left = index * 2 + 1;
while (left < size) {
int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;
largest = arr[largest] > arr[index] ? largest : index;
if (largest == index) {
break;
}
int temp = arr[index];
arr[index] = arr[largest];
arr[largest] = temp;
index = largest;
left = index * 2 + 1;
}
}
|
合并 K 个排序链表
23. 合并 K 个升序链表
问题
【LeetCode 23】:给你一个链表数组,每个链表都已经按升序排列。
小顶堆合并
- 维护当前每个链表未合并的元素的最前面一个,k 个链表就最多有 k 个满足这样条件的元素
- 每次在这些元素里面选取 val 属性最小的元素合并到答案中
- 使用小顶堆数据结构选取最小元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
PriorityQueue<ListNode> queue;
public ListNode mergeKLists(ListNode[] lists) {
queue = new PriorityQueue<>(Comparator.comparing(listNode -> listNode.val));
for (ListNode node : lists) {
if (node != null) {
queue.offer(node);
}
}
ListNode L = new ListNode(0);
ListNode tail = L;
while (!queue.isEmpty()) {
tail.next = queue.poll();
tail = tail.next;
if (tail.next != null) {
queue.offer(tail.next);
}
}
return L.next;
}
|
数据流的中位数
通关进度
295. 数据流的中位数
问题
【LeetCode 295】:中位数是有序整数列表中的中间值。如果列表的大小是偶数,则没有中间值,中位数是两个中间值的平均值。
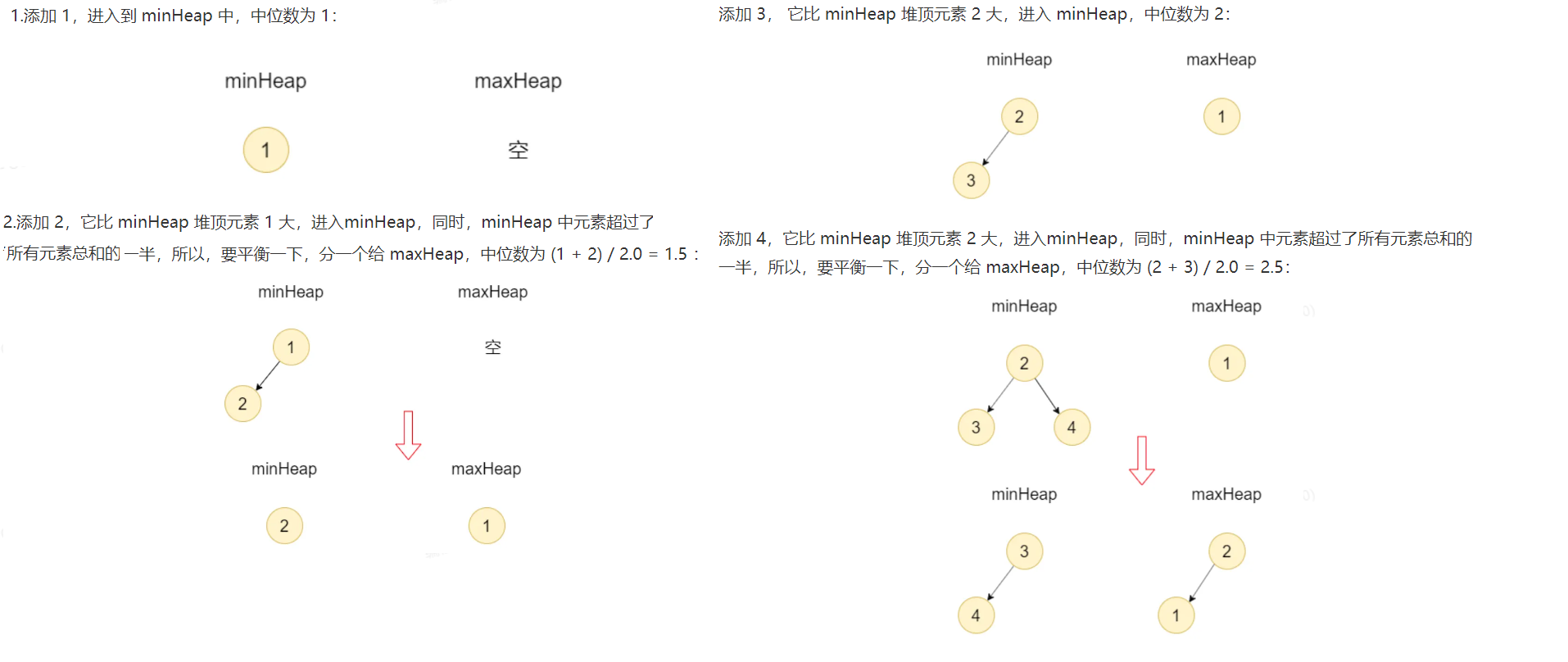
左边大顶堆,右边小顶堆,小的加左边,大的加右边,平衡俩堆数,新加就弹出,堆顶给对家,奇数取多的,偶数取除2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
PriorityQueue<Integer> minHeap;
PriorityQueue<Integer> maxHeap;
public MedianFinder() {
this.minHeap = new PriorityQueue<>();
this.maxHeap = new PriorityQueue<>((a, b) -> (b - a));
}
public void addNum(int num) {
if (minHeap.isEmpty() || num > minHeap.peek()) {
minHeap.offer(num);
if (minHeap.size() - maxHeap.size() > 1) {
maxHeap.offer(minHeap.poll());
}
} else {
maxHeap.offer(num);
if (maxHeap.size() - minHeap.size() > 0) {
minHeap.offer(maxHeap.poll());
}
}
}
public double findMedian() {
if (minHeap.size() > maxHeap.size()) {
return minHeap.peek();
} else if (minHeap.size() < maxHeap.size()) {
return maxHeap.peek();
} else {
return (maxHeap.peek() + minHeap.peek()) / 2.0;
}
}
|




















