算法通关 15 - 超大规模数据场景题
大数据类型题目技巧
- 哈希函数可以把数据按照种类均匀分流
- 布隆过滤器用于集合的建立与查询,并可以节省大量空间
- 一致性哈希解决数据服务器的负载管理问题
- 利用并查集结构做岛问题的并行计算
- 位图解决某一范围上数字的出现情况,并可以节省大量空间
- 利用分段统计思想、并进一步节省大量空间
- 利用堆、外排序来做多个处理单元的结果合并
用 4 KB 内存寻找重复元素
通关进度
| 题目 | 说明 |
|---|---|
| 用 4 KB 内存寻找重复元素 | 通关 |
参考资料
海量场景思路
- 位存储
- 文件分块,时间换空间
- 堆,第 K 大/小, K 个最大/最小(查小用大堆,查大用小堆)
问题
给定 1~N 的数组,N 最大 32000,其中存在重复值,在内存 4KB 的情况下找出所有重复元素
位运算
使用 Bitmap,对于 4kb 空间寻址范围为 $8\times{4}\times2^{10}$,完全满足题目所需。
【仅供参考】1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46class BitSet {
int[] bits;
public BitSet(int size) {
this.bits = new int[size >> 5];
}
// 判断 pos 位置的数是否出现过
boolean get(int pos) {
// / 32
int posBit = (pos >> 5);
// % 32
int bitNumber = (pos & 0x1F);
return (bits[posBit] & (1 << bitNumber)) != 0;
}
// 将 pos 位置的值设置为 1
void set(int pos) {
// / 32
int posBit = (pos >> 5);
// % 32
int bitNumber = (pos & 0x1F);
bits[posBit] = bits[posBit] | (1 << bitNumber);
}
}
public void checkDuplicatedNum(int[] number) {
BitSet bitset = new BitSet(32000);
for (int i = 0; i < number.length; i++) {
int num = number[i]; // 数组范围 [1, N]
int postion = num - 1; // num 在 bitmap 数组下标
if (bitset.get(postion)) {
// Visit()
System.out.println(num);
} else { // 第一次出现
bitset.set(postion);
}
}
}
海量数据场景题
通关进度
| 题目 | 说明 |
|---|---|
| “40”亿个非负整数中找到未出现的数 | 通关 |
| 搜索词汇的 Top K 问题 | 通关 |
| 找到”100”亿个 URL 中重复的 URL | 通关 |
| “40”亿个非负整数中找到出现两次的数和所有数的中位数 | 通关 |
| 使用 2 GB 内存在20 亿整数中找出现次数最多的数 | 通关 |
“40”亿个非负整数中找到未出现的数
32 位无符号整数的范围是 0~4,294,967,295,现在有 40 亿个无符号整数,可以使用最多 1 GB 的内存,找出所有出现两次的数。
常态问题
哈希表不适合作为存储结构的原因
假设使用哈希表保存出现过的数,如果40亿个数不同,则哈希表的记录数为40亿条,存一个32位整数需要4B,最差情况需要$40亿*4B=160亿KB≈16GB$,远远不符合要求
使用位图作为存储结构
使用 bit map 表示数出现的情况,申请长度为 4,294,967,295 的 bit 数组 bitArr,bitArr 上每个位置表示 0 或 1 状态。8 bit = 1 B,长度为 4,294,967,295 的 bit 类型数组占用 500MB
遍历 40 亿 无符号整数,遇到所有的数时就把 bitArr[] 相应位置置 1(假设遇到 7000,就把 bitArr[7000] 置1)
遍历完,再次遍历 bitArr,哪个位置没有置 1,这个数就不在这 40 亿数中(假设 bitArr[8000]=0,那么 8000 就是没出现过的数)
进阶问题
内存限制为10MB,但是只需找到一个没出现的数即可。
分析
40 亿需要 500 MB 空间,如果只有 10 MB,至少需要 50 块内存,由于分块一般是 2 的幂
分块
- 0 ~ 4,294,967,295 是可以平均分成 64 个区间,每个区间 67,108,864 个数
- 第
0区间0 ~ 67,108,863 - 第
1区间67,108,864 ~ 134,217,728 - 第
i区间67,108,864 × i ~ 67,108,864 × (i+1) - 1) - 第
63区间4,227,858,432 ~ 4,294,967,295
一共有 40亿 个数,如果统计落在每一个区间上的数,肯定至少一个区间的计数少于 67,108,864,利用这点找到其中一个没出现的数
第一次遍历
第一次遍历先申请长度为 64 的整型数组
countArr[0...63],countArr[i]用来统计区间i上的数遍历 40 亿个数,根据当前数多少决定在哪个区间上计数增加
如果当前数是
3422,552,090,3422,552,090/67,108,864=51,所以第51区间计数增加countArr[51]++遍历完 40 亿数后,遍历
countArr,必然有一个位置countArr[i]小于67,108,864,表示第 i 区间至少一个数没出现过第一次遍历使用的内存 $64*4B$
第二次遍历
假设找到第 37 区间的计数小于 67,108,864,以下是第二次遍历
- 申请长度为
67,108,864的 bitmap(约占用 8 MB),记为bitArr[0..67,108,863] - 再遍历一次 40 亿个数,此时遍历只关注落在第
37个数,记为 num(num/67,108,864=37),其他区间的数全都忽略 - 如果步骤2的 num 在第
37区间上,将bitArr[num-67,108,864*37]的值设置成1。只做第37区间上的数的bitArr映射 - 遍历完 40 亿个数后,在
bitArr上必然存在没有设置成1的位置,假设第i位置上的值没有设置成1,那么67,108,864 × 37 + i这个数就是一个没出现过的数
总结
- 根据 10 MB 的内存限制,确定 区间统计 的大小,就是第二次遍历时的 bitArr 大小
- 利用区间计数的方式,找到计数不足的区间,这个区间肯定有没出现的数
- 对这个区间的数 做 bitmap 映射,再遍历 bitmap,找到一个没出现的数即可
搜索词汇的 Top K 问题
问题
某搜索公司一天的用户搜索词汇是海量的(百亿数据量),请设计一种求出每天热门 Top100 词汇的可行办法
方法 1 哈希分流+小根堆
- 把包含百亿数据量的词汇文件分流到不同的机器上,对每台机器来说,如果分到的数据量依然很大(比如内存不够或存在其他问题,再用哈希函数把每台机器的分流文件拆成更小的文件处理)
- 处理每个小文件时,通过哈希表统计每种词及词频
- 哈希表建立完成后,再遍历哈希表,遍历哈希表的过程中使用大小为
100的小根堆选出每个小文件的Top 100(整体未排序的Top 100) - 每个小文件都有自己词频的小根堆(整体未排序的Top100),将小根堆的词按照词频排序,得到排序后的
Top 100 - 把各个文件排序后的
Top 100进行外排序或者继续利用小根堆,就可以选出每台机器上的Top 100 - 不同机器之间的
Top 100再进行外排序或利用小根堆 - 最终求出整个百亿数据量中的
Top 100
方法 2 哈希分流+大根堆
- 把包含百亿数据量的词汇文件分流到不同的机器上,对每台机器来说,如果分到的数据量依然很大(比如内存不够或存在其他问题,再用哈希函数把每台机器的分流文件拆成更小的文件处理)
- 处理每个小文件时,通过哈希表统计每种词及词频
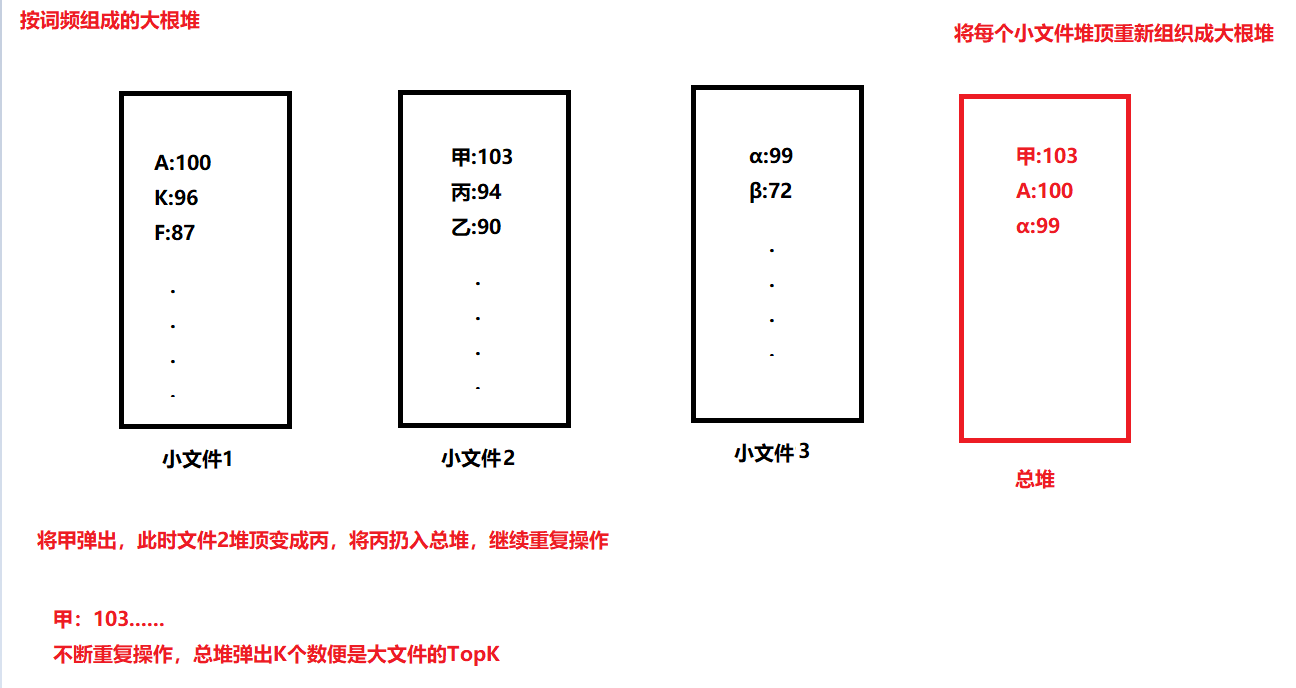
总结
分流是处理大数据的不错方案:
- 哈希函数将大文件内容分配给不同机器
- 用哈希函数把大文件拆成小文件,处理每个小数量的集合
大数据经典TopK问题:
- 哈希函数分流
- 哈希表做词频统计
- 堆结构和外排序处理
思路剖析
哈希分流成小文件>>小文件词频统计,存储在哈希表中>>小文件计算出各自的TopK>>每个小文件的TopK进行汇总排序,得到大文件的TopK>>每个排序后的大文件的TopK进行排序,得到每台机器的TopK>>不同机器的TopK再排序>>得到全局TopK
找到”100”亿个 URL 中重复的 URL
问题
有一个包含100亿个 URL 的大文件,假设每个 URL 占用64B,请找出其中所有重复的 URL
常规思路
把大文件通过哈希函数分配到机器,或者通过哈希函数把大文件拆成小文件,一直进行划分,直到划分的结果满足资源限制
弄清楚资源限制(内存、计算时间),明确要求后将每条 URL 通过哈希函数分配到若干机器或拆分成若干小文件(若干指具体资源限制计算出精确的数量)
- 例如,将100亿个的大文件通过哈希函数分配到
100台机器上,然后每台机器分别统计分给自己的 URL 是否有重复的URL,同时哈希函数的性质决定同一条 URL 可能分配给不同机器 - 或者,在单机上将大文件通过哈希函数拆成
1000个小文件,对每一个小文件再利用哈希表遍历,找出重复的 URL - 或者,在分给机器或拆完文件之后排序,排序过后再看是否有重复的URL出现
“40”亿个非负整数中找到出现两次的数和所有数的中位数
寻找出现两次的数字
问题
32 位无符号整数的范围是 0~4,294,967,295,现在有40亿个无符号整数,可以使用最多1GB的内存,找出所有出现两次的数。
算法思路
使用 bitmap,用两个位置表示一个数的词频,01 表示该数出现一次,10 表示该数出现两次,11 表示该数出现三次及以上,1B 占用 8bit,长度为 4,294,967,295×2 的 bit 型数组占用1GB
算法实现
- 遍历 40亿 个无符号整数,初次遇到
num,bitArr[num × 2+1]和bitArr[num × 2]设置成0、1 - 第二次遇到
num,bitArr[num × 2+1]和bitArr[num × 2]设置成1、0 - 第三次遇到
num,bitArr[num × 2+1]和bitArr[num × 2]设置成1、1 - 以后再遇到
num,发现此时bitArr[num × 2+1]和bitArr[num × 2]已经被设置成1、1,就不再做任何设置 - 遍历完成后,再次遍历
bitArr,如果发现bitArr[num × 2+1]和bitArr[num × 2]被设置成1、0,那么num就是出现两次的数寻找中位数
问题
可以使用最多 10KB 的内存,怎么找到这 40 亿个整数的中位数?

采用区间统计的方式
- 根据内存大小和无符号整数数组大小确定分配数组长度
- 遍历40亿数据,
arr[i]表示第i区间有多少数 - 通过累加每个区间的出现次数,能找到第20亿个数落在哪个区间
- 比如
0~k-1区间上的数出现了18亿,当发现加上第k区间的数超过了20亿,就可以知道第20亿数是第k区间上的数,并且可以知道是第k区间上的第2亿个数 - 接下来申请单个区间长度
L的无符号整型数组 - 遍历 40亿 个数,只关心处在第
k区间的数,记为num,将count[num-k*L]++(对第k区间做词频统计) - 最后只在第
k区间找第2亿个数即可
使用 2 GB 内存在20 亿整数中找出现次数最多的数
题目
在包含 20 亿个全是 32 位整数的大文件中找到出现次数最多的数,内存限制为 2 GB
解决方案
将 20 亿个文件经哈希函数分流成 16 个小文件,根据哈希函数悉尼告知,同一种数不可能被散列到不同小文件中,同时每个小文件不同的数一定不会大于 2 亿
假如哈希函数足够优秀看,我们对每个小文件使用哈希表统计出现次数,接下来选出 16 个小文件各自的 TOP 1 即可
超大规模数据场景题
通关进度
| 题目 | 说明 |
|---|---|
| 对 20 文件进行排序 | 通关 |
| 超大文本中搜索两个单词的最短距离 | 通关 |
| 在 100 亿数字中寻找最小的 100 万个数字 | 通关 |
对 20 文件进行排序
题目要求
假设有 20 GB 文件,每行一个字符串,请对该文件进行排序
外部排序
将文件划分成若干块,每块大小 XMB,先对每块排序,然后再合并,K 归并
超大文本中搜索两个单词的最短距离
题目
给定超大文本文件,内部由若干单词组成。现在给定两个单词,请你找出这两个单词在文件中的最小距离
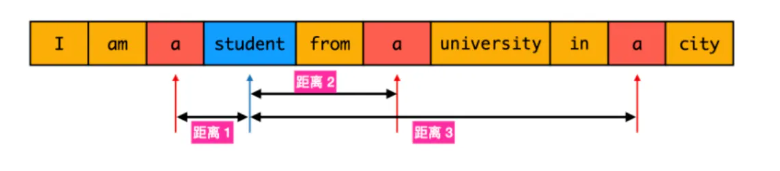
解决方案
- 遍历到 $word_1$ 和 $word_2$ 时记录其位置
- 当遍历到 $word_1$ 时,如果已经遍历的单词中存在 $word_2$,为计算最短距离,取最后一个已遍历的 $word_2$ 位置,并计算和当前下标的距离
- 同理,当遍历到 $word_2$ 时,取最后一个已遍历的 $word_1$ 位置,并计算和当前下标的距离

在 100 亿数字中寻找最小的 100 万个数字
问题
在 100 亿数字中寻找最小的 100 万个数字
查小用大堆,查大用小堆
- 为前 100 万数据创建大堆,最大元素位于堆顶
- 遍历整个序列,只有比堆顶元素小的才允许插入堆中,并删除原堆的最大元素
- 之后继续遍历剩下的数字,最后只剩下最小的 100 万









