通关进度

题目 说明
子数组最大平均数 通关
最长连续递增序列 通关

参考资料

滑动窗口思想简介

滑动窗口入门题

固定窗口

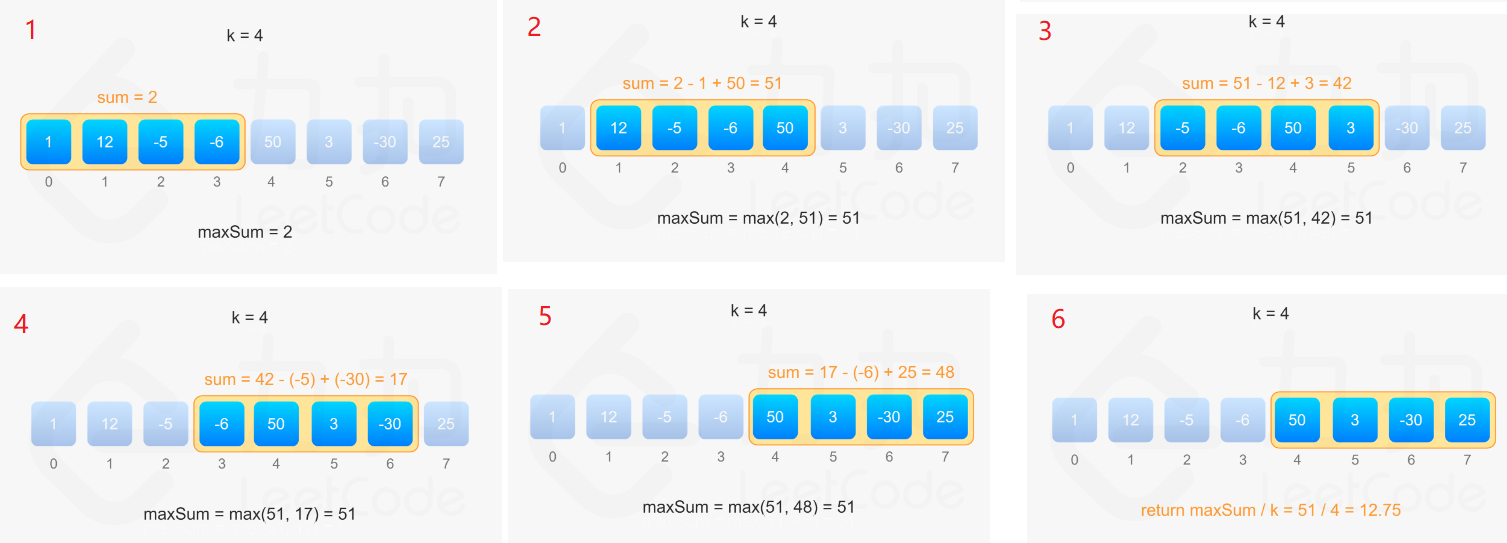
643. 子数组最大平均数 I

问题

给你一个由 n 个元素组成的整数数组 nums 和一个整数 k 。

请你找出平均数最大且 长度为 k 的连续子数组，并输出该最大平均数。

滑动窗口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 固定窗口大小
public double findMaxAverage(int[] nums, int k) {

    int sum = 0;
    int n = nums.length;

    // 计算初始窗口的值，窗口大小 k
    for (int i = 0; i < k; i++) {
        sum += nums[i];
    }
    int maxSum = sum;
    // 窗口右移动：end++
    for (int end = k; end < n; end++) {
        sum = sum - nums[end - k] + nums[end];
        maxSum = Math.max(maxSum, sum);
    }
    return 1.0 * maxSum / k;
}

可变窗口

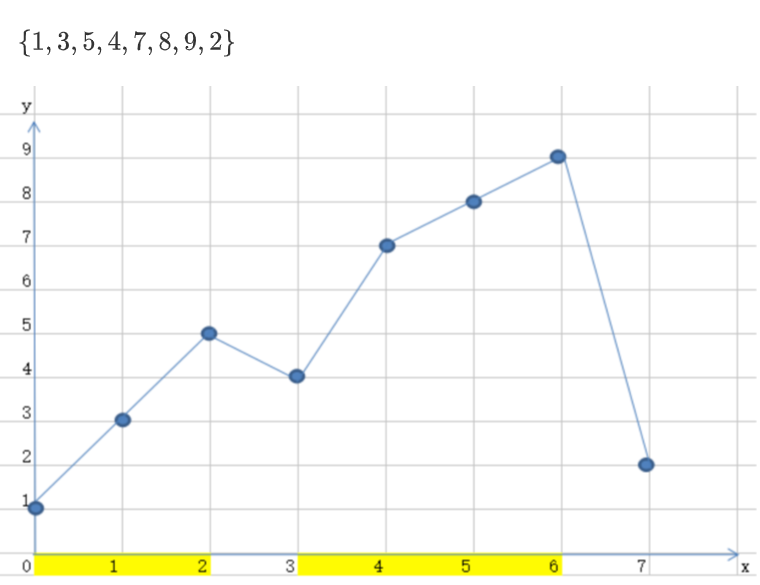
674. 最长连续递增序列

问题

给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度

滑动窗口

1
2
3
4
5
6
7
8
9
10
11
12
public int findLengthOfLCIS(int[] nums) {
    int ans = 0;
    int n = nums.length;
    int start = 0;
    for (int i = 0; i < n; i++) {
        if (i > 0 && nums[i] <= nums[i - 1]) {
            start = i;
        }
        ans = Math.max(ans, i - start + 1);
    }
    return ans;
}

滑动窗口经典题

通关进度

题目 说明
最长子串专题 通关
长度最小的子数组 通关
盛水最多的容器 通关
子串异位词专题 通关

推荐阅读

我写了一首诗，把滑动窗口算法变成了默写题

最长子串专题

无重复字符的最长子串

3. 无重复字符的最长子串

问题

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 长度

滑动窗口

以 abcabcbb 为例，找出从每一个字符开始的，不包含重复字符的最长子串，那么其中最长的那个字符串即为答案。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public int lengthOfLongestSubstring(String s) {
    // 哈希集合，记录每个字符是否出现过
    Set<Character> occ = new HashSet<Character>();
    int n = s.length();
    // 右指针，初始值为 -1，相当于我们在字符串的左边界的左侧，还没有开始移动
    int rk = -1, ans = 0;
    for (int i = 0; i < n; ++i) {
        if (i != 0) {
            // 左指针向右移动一格，移除一个字符
            occ.remove(s.charAt(i - 1));
        }
        while (rk + 1 < n && !occ.contains(s.charAt(rk + 1))) {
            // 不断地移动右指针
            occ.add(s.charAt(rk + 1));
            ++rk;
        }
        // 第 i 到 rk 个字符是一个极长的无重复字符子串
        ans = Math.max(ans, rk - i + 1);
    }
    return ans;
}

hashMap

哈希解决方案

至多包含两个不同字符的最长子串

159. 至多包含两个不同字符的最长子串

问题

给定一个字符串 s ，找出 至多 包含两个不同字符的最长子串 t 。 

1
2
3
4
5
6
7
输入: "eceba"
输出: 3
解释: t 是 "ece"，长度为3。

输入: "ccaabbb"
输出: 5
解释: t 是 "aabbb"，长度为5。

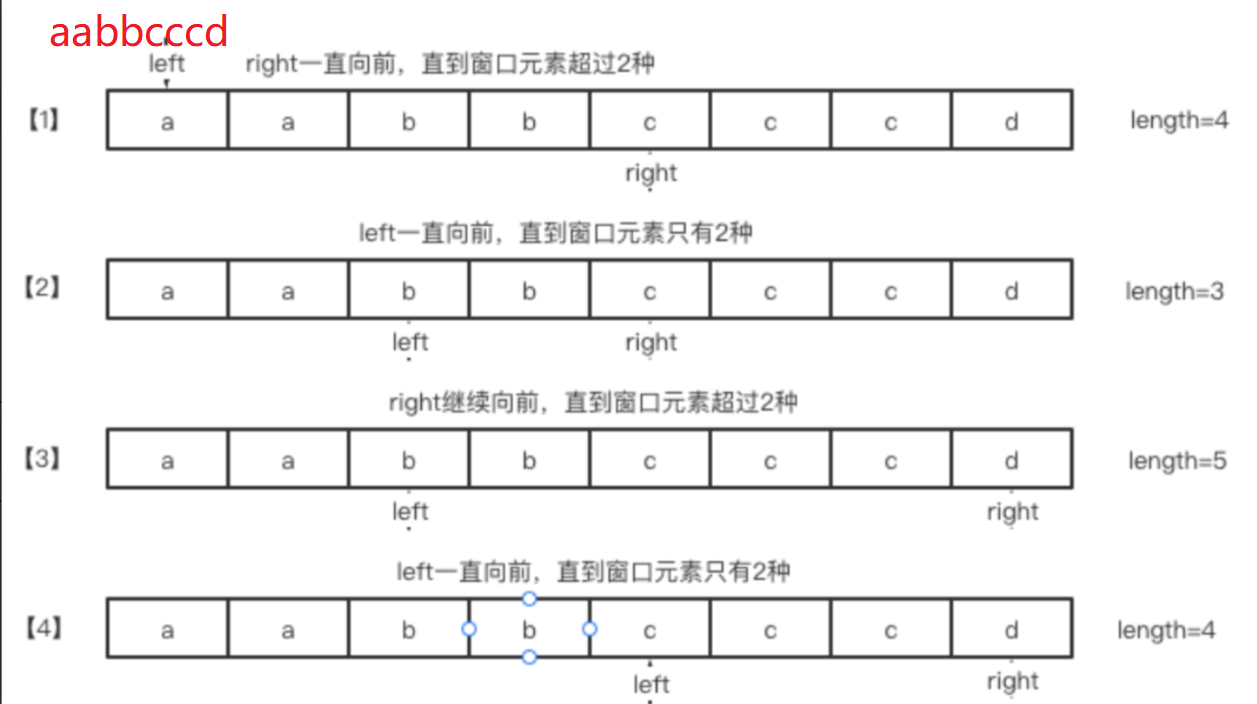
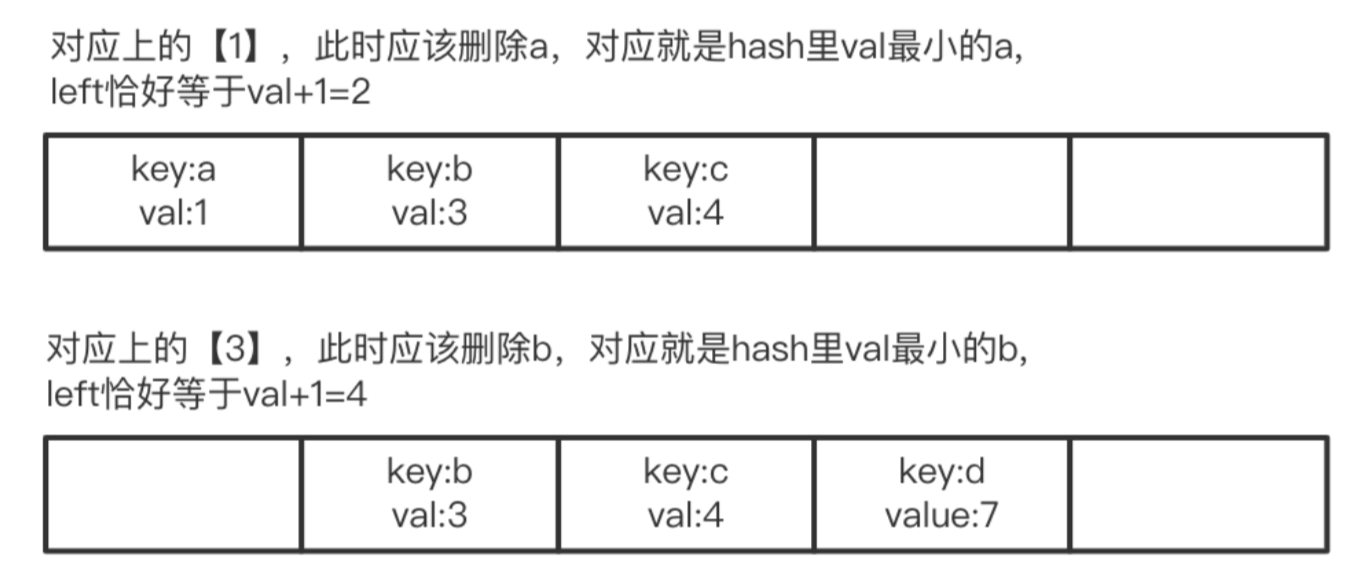
算法思路

问题突破口：

  1. 判断只有两个元素
  2. 考虑移除的元素

解决方案：

  1. 键：字符串中的字符
  2. 值：滑动窗口中的最右边的字符位置

使用如下方案确定需要删除的元素和窗口 left 的新位置：

1
2
3
// 从哈希中找最小值
del_idex = Collections.min(hashmap.values());
left = del_idex + 1;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public int lengthOfLongestSubStringTwoDistinct(String s) {
    if (s.length() < 3) {
        return s.length();
    }
    int left = 0, right = 0;
    Map<Character, Integer> hashMap = new HashMap<>();
    int maxLen = 2;

    while (right < s.length()) {
        if (hashMap.size() < 3) {
            hashMap.put(s.charAt(right), right++);
        }
        // 如果数量达到 3
        if (hashMap.size() == 3) {
            // 最左侧待删除的为止
            int del_idex = Collections.min(hashMap.values());
            hashMap.remove(s.charAt(del_idex));
            // 窗口 left 的新位置
            left = del_idex + 1;
        }
        maxLen = Math.max(maxLen, right - left);
    }
    return maxLen;
}

至多包含 K 个不同字符的最长子串

至多包含 K 个不同字符的最长子串

问题

给定一个字符串 s ，找出 至多 包含 K 个不同字符的最长子串 t 。 

1
2
3
输入: "eceba", k = 2 
输出: 3
解释: t 是 "ece"，长度为 3。

算法思想

只要将判断 hashMap 数量大小改为 $k$，超过 $2$ 就是 $k+1$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public int lengthOfLongestSubStringKDistinct(String s, int k) {
    if (s.length() < k + 1) {
        return s.length();
    }
    int left = 0, right = 0;
    Map<Character, Integer> hashMap = new HashMap<>();
    int maxLen = k;

    while (right < s.length()) {
        if (hashMap.size() < k + 1) {
            hashMap.put(s.charAt(right), right++);
        }
        // 如果数量达到 3
        if (hashMap.size() == k + 1) {
            // 最左侧待删除的为止
            int del_idex = Collections.min(hashMap.values());
            hashMap.remove(s.charAt(del_idex));
            // 窗口 left 的新位置
            left = del_idex + 1;
        }
        maxLen = Math.max(maxLen, right - left);
    }
    return maxLen;
}

长度最小的子数组

209. 长度最小的子数组

问题

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

标准答案

查看答案

盛水最多的容器

11. 盛最多水的容器

问题

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

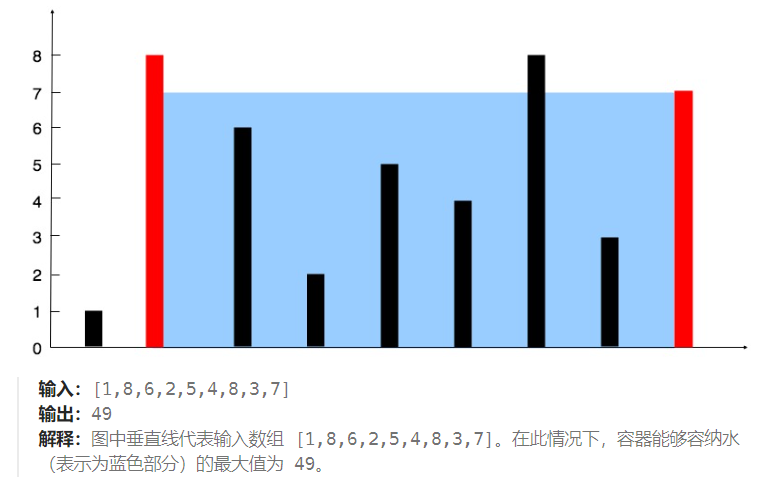
算法思想

现有双指针 $i,j$，指向的水槽板高度分别为 $h[i]，h[j]$，此状态下水槽面积为 $S(i,j)$。由于可容纳水的高度由两板中的短板决定，因此：

在每个状态下，无论长板或短板向中间收窄一格，都会导致水槽底边宽度−1 变短：

  • 若向内移动短板 ，水槽的短板 min(h[i],h[j]) 可能变大，因此下个水槽的面积可能增大

  • 若向内移动长板 ，水槽的短板 min(h[i],h[j])不变或变小，因此下个水槽的面积一定变小

    因此，只要初始化双指针分列水槽左右两端，循环每轮将短板向内移动一格，并更新面积最大值，直到两指针相遇时跳出；即可获得最大面积 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int maxArea(int[] height) {
    int l = 0, r = height.length - 1;
    int ans = 0;
    while (l < r) {
        int area = Math.min(height[l], height[r]) * (r - l);
        ans = Math.max(ans, area);
        if (height[l] <= height[r]) {
            ++l;
        }
        else {
            --r;
        }
    }
    return ans;
}

【排列】子串异位词专题

字符串的排列

567. 字符串的排列

问题

给你两个字符串 s1 和 s2 ，写一个函数来判断 s2 是否包含 s1 的排列。如果是，返回 true ；否则，返回 false 。

换句话说，s1 的排列之一是 s2 的 子串 。

1
2
3
输入：s1 = "ab" s2 = "eidbaooo"
输出：true
解释：s2 包含 s1 的排列之一 ("ba").

滑动窗口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public boolean checkInclusion(String s1, String s2) {
    int n = s1.length(), m = s2.length();
    if (n > m) {
        return false;
    }
    int[] cnt1 = new int[26];
    int[] cnt2 = new int[26];
    for (int i = 0; i < n; ++i) {
        ++cnt1[s1.charAt(i) - 'a'];
        ++cnt2[s2.charAt(i) - 'a'];
    }
    if (Arrays.equals(cnt1, cnt2)) {
        return true;
    }
    for (int i = n; i < m; ++i) {
        ++cnt2[s2.charAt(i) - 'a'];
        --cnt2[s2.charAt(i - n) - 'a'];
        if (Arrays.equals(cnt1, cnt2)) {
            return true;
        }
    }
    return false;
}

找到字符串中所有字母异位词

438. 找到字符串中所有字母异位词

问题

给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

异位词 指由相同字母重排列形成的字符串（包括相同的字符串）

1
2
3
4
5
输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。

算法思想

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public List<Integer> findAnagrams(String s, String p) {
    int sLen = s.length(), pLen = p.length();

    if (sLen < pLen) {
        return new ArrayList<Integer>();
    }

    List<Integer> ans = new ArrayList<Integer>();
    int[] sCount = new int[26];
    int[] pCount = new int[26];
    for (int i = 0; i < pLen; ++i) {
        ++sCount[s.charAt(i) - 'a'];
        ++pCount[p.charAt(i) - 'a'];
    }

    if (Arrays.equals(sCount, pCount)) {
        ans.add(0);
    }

    for (int i = 0; i < sLen - pLen; ++i) {
        --sCount[s.charAt(i) - 'a'];
        ++sCount[s.charAt(i + pLen) - 'a'];

        if (Arrays.equals(sCount, pCount)) {
            ans.add(i + 1);
        }
    }

    return ans;
}

滑动窗口最大值

239. 滑动窗口最大值

问题

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 

1
2
3
4
5
6
7
8
9
10
11
输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

优先队列

算法思想

本题初始时，我们将数组 nums 的前 k个元素放入优先队列中。每当我们向右移动窗口时，我们就可以把一个新的元素放入优先队列中，此时堆顶的元素就是堆中所有元素的最大值。然而这个最大值可能并不在滑动窗口中，在这种情况下，这个值在数组 nums 中的位置出现在滑动窗口左边界的左侧。因此，当我们后续继续向右移动窗口时，这个值就永远不可能出现在滑动窗口中了，我们可以将其永久地从优先队列中移除。

我们不断地移除堆顶的元素，直到其确实出现在滑动窗口中。此时，堆顶元素就是滑动窗口中的最大值。为了方便判断堆顶元素与滑动窗口的位置关系，我们可以在优先队列中存储二元组 (num,index)，表示元素num 在数组中的下标为index。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public int[] maxSlidingWindow(int[] nums, int k) {
    int n = nums.length;
    PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>() {
        public int compare(int[] pair1, int[] pair2) {
            return pair1[0] != pair2[0] ? pair2[0] - pair1[0] : pair2[1] - pair1[1];
        }
    });
    for (int i = 0; i < k; ++i) {
        pq.offer(new int[]{nums[i], i});
    }
    int[] ans = new int[n - k + 1];
    ans[0] = pq.peek()[0];
    for (int i = k; i < n; ++i) {
        pq.offer(new int[]{nums[i], i});
        while (pq.peek()[1] <= i - k) {
            pq.poll();
        }
        ans[i - k + 1] = pq.peek()[0];
    }
    return ans;
}

单调队列

算法思想

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// 单调队列
public int[] maxSlidingWindow(int[] nums, int k) {
    int n = nums.length;
    Deque<Integer> deque = new LinkedList<Integer>();
    for (int i = 0; i < k; ++i) {
        while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {
            deque.pollLast();
        }
        deque.offerLast(i);
    }

    int[] ans = new int[n - k + 1];
    ans[0] = nums[deque.peekFirst()];
    for (int i = k; i < n; ++i) {
        while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {
            deque.pollLast();
        }
        deque.offerLast(i);
        while (deque.peekFirst() <= i - k) {
            deque.pollFirst();
        }
        ans[i - k + 1] = nums[deque.peekFirst()];
    }
    return ans;
}